Question Number 197132 by Erico last updated on 08/Sep/23
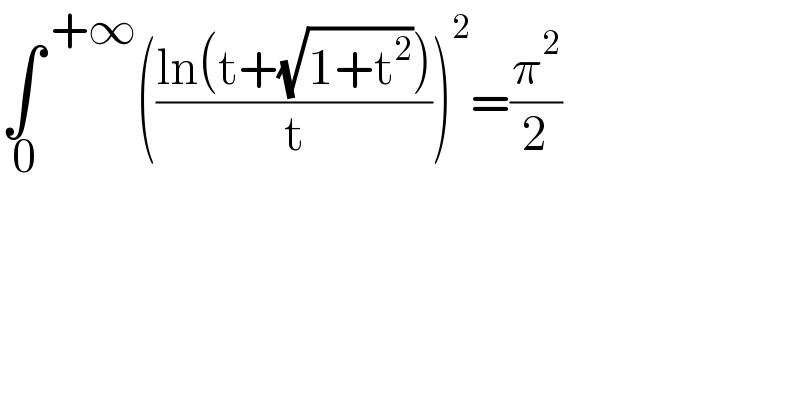
$$\underset{\:\mathrm{0}} {\int}^{\:+\infty} \left(\frac{\mathrm{ln}\left(\mathrm{t}+\sqrt{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\right)}{\mathrm{t}}\right)^{\mathrm{2}} =\frac{\pi^{\mathrm{2}} }{\mathrm{2}} \\ $$
Commented by mnjuly1970 last updated on 09/Sep/23
$$\:\:\:\:{ti}\:{tok}\:{agha}\:{sardool}\:.. \\ $$
Answered by witcher3 last updated on 09/Sep/23
![t=sh(x) ∫_0 ^∞ ((x/(sh(x))))^2 ch(x)dx =∫_0 ^∞ (x^2 /(sh^2 (x)))ch(x)=lim_((a,b)→(0,∞)) [−(x^2 /(sh(x)))]_a ^b +∫_0 ^∞ ((2x)/(sh(x)))dx =2∫_0 ^∞ ((2x)/(e^x −e^(−x) ))dx =∫_0 ^∞ ((4xe^(−x) )/(1−e^(−2x) ))dx =4Σ_(n≥0) ∫_0 ^∞ xe^(−(1+2n)x) dx=Σ_(n≥0) (4/((1+2n)^2 )) =4(ζ(2)−(1/4)ζ(2))=(π^2 /2)](https://www.tinkutara.com/question/Q197163.png)
$$\mathrm{t}=\mathrm{sh}\left(\mathrm{x}\right) \\ $$$$\int_{\mathrm{0}} ^{\infty} \left(\frac{\mathrm{x}}{\mathrm{sh}\left(\mathrm{x}\right)}\right)^{\mathrm{2}} \mathrm{ch}\left(\mathrm{x}\right)\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{sh}^{\mathrm{2}} \left(\mathrm{x}\right)}\mathrm{ch}\left(\mathrm{x}\right)=\underset{\left(\mathrm{a},\mathrm{b}\right)\rightarrow\left(\mathrm{0},\infty\right)} {\mathrm{lim}}\left[−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{sh}\left(\mathrm{x}\right)}\right]_{\mathrm{a}} ^{\mathrm{b}} +\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{2x}}{\mathrm{sh}\left(\mathrm{x}\right)}\mathrm{dx} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{2x}}{\mathrm{e}^{\mathrm{x}} −\mathrm{e}^{−\mathrm{x}} }\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{4xe}^{−\mathrm{x}} }{\mathrm{1}−\mathrm{e}^{−\mathrm{2x}} }\mathrm{dx} \\ $$$$=\mathrm{4}\underset{\mathrm{n}\geqslant\mathrm{0}} {\sum}\int_{\mathrm{0}} ^{\infty} \mathrm{xe}^{−\left(\mathrm{1}+\mathrm{2n}\right)\mathrm{x}} \mathrm{dx}=\underset{\mathrm{n}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{4}}{\left(\mathrm{1}+\mathrm{2n}\right)^{\mathrm{2}} } \\ $$$$=\mathrm{4}\left(\zeta\left(\mathrm{2}\right)−\frac{\mathrm{1}}{\mathrm{4}}\zeta\left(\mathrm{2}\right)\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{2}} \\ $$
