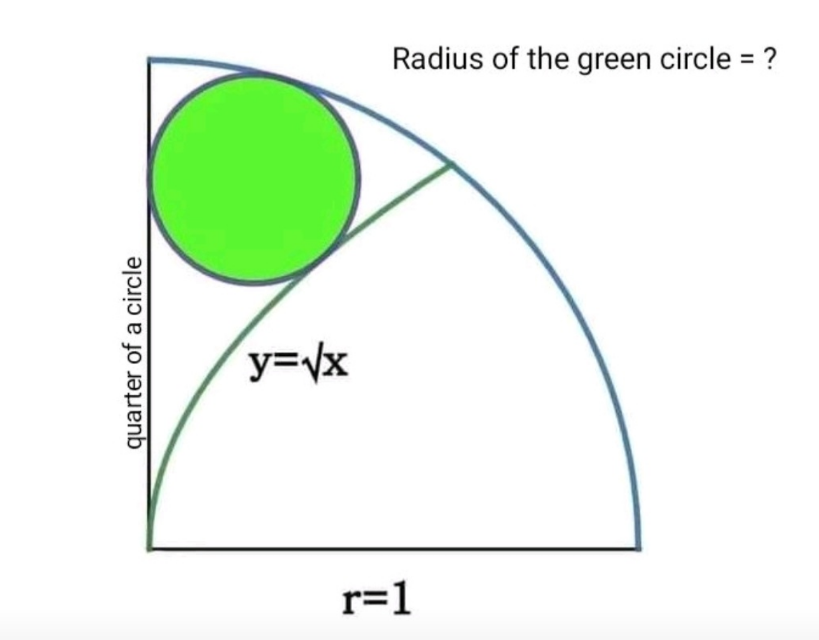
Question Number 197128 by Mingma last updated on 08/Sep/23
Commented by Frix last updated on 09/Sep/23

$$\mathrm{I}\:\mathrm{get}\:\rho\approx.\mathrm{213841779235} \\ $$
Answered by sniper237 last updated on 09/Sep/23

$${The}\:{circle}\:{is}\:\:{embedded}\:{in}\:{the}\:{triangle} \\ $$$${formed}\:{by}\:{the}\:{intersection}\:{points}\:{of}\:\: \\ $$$$\:{curves}\:\:{y}=\sqrt{{x}\:}\:;\:{y}=\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:\:{and}\:{y}=\mathrm{0}\: \\ $$$${They}\:{are}\:{A}\left(\mathrm{0},\mathrm{0}\right),\:{B}\left(\mathrm{0},\mathrm{1}\right)\:,{C}\left(\varphi^{−\mathrm{1}} ,\sqrt{\varphi}\:\right).\:{Let}\:\: \\ $$$${O},\:{r},\:{the}\:{center}\:{and}\:{radius}\:{of}\:{the}\:{circle} \\ $$$${For}\:{each}\:{triangle}\:{OAB},{OAC},{OBC}\: \\ $$$${the}\:{morgue}\:{is}\:{r}.\:{So}\:\:{if}\:{S}\:{is}\:{ABC}\:{area} \\ $$$$\frac{{r}×{AB}}{\mathrm{2}}+\frac{{r}×{AC}}{\mathrm{2}}+\frac{{r}×{BC}}{\mathrm{2}}={S} \\ $$$${then}\:\:{r}\:=\:\frac{\mathrm{2}{S}}{{AB}+{AC}+{BC}} \\ $$$$\:\:{ABC}={D}=\left\{\:\left({x},{y}\right)/\:\sqrt{{x}}\:\leqslant{y}\leqslant\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:\right\} \\ $$$${So}\:\:{S}=\:\int\int_{{D}} {dxdy}=\int_{\mathrm{0}} ^{\varphi^{−\mathrm{1}} } \left(\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:−\sqrt{{x}}\:\right){dx} \\ $$
