Menu Close

sir-number-of-3-digit-numbers-which-are-divisible-by-a-3-b-4-c-6-d-7-e-8-f-9-g-11-when-repetetion-is-1-Allowwd-2-Not-allowed-kindly-help-me-sir-

Tinku Tara 0 Comments
Pin




Question Number 197564 by SLVR last updated on 21/Sep/23
sir...number of 3 digit numbers which are divisible by a)3 b)4 c)6 d)7 e)8 f)9 g)11 when repetetion is 1)Allowwd 2)Not allowed.. kindly help me sir
$${sir}…{number}\:{of}\:\mathrm{3}\:{digit} \\ $$$${numbers}\:{which}\:{are}\:{divisible} \\ $$$${by}\: \\ $$$$\left.{a}\left.\right)\left.\mathrm{3}\left.\:\left.\:\left.{b}\left.\right)\mathrm{4}\:\:{c}\right)\mathrm{6}\:\:{d}\right)\mathrm{7}\:\:{e}\right)\mathrm{8}\:\:{f}\right)\mathrm{9}\:\:{g}\right)\mathrm{11} \\ $$$${when}\:{repetetion}\:{is} \\ $$$$\left.\mathrm{1}\left.\right){Allowwd}\:\:\mathrm{2}\right){Not}\:{allowed}.. \\ $$$${kindly}\:{help}\:{me}\:{sir} \\ $$
Commented by Tinku Tara last updated on 21/Sep/23
All numbers are divisble by one. check your question
$$\mathrm{All}\:\mathrm{numbers}\:\mathrm{are}\:\mathrm{divisble}\:\mathrm{by}\:\mathrm{one}. \\ $$$$\mathrm{check}\:\mathrm{your}\:\mathrm{question} \\ $$
Commented by SLVR last updated on 21/Sep/23
i am sorry by 1 was wrogly typed
$${i}\:{am}\:{sorry}\:{by}\:\mathrm{1}\:{was}\:{wrogly}\:{typed} \\ $$
Commented by JDamian last updated on 22/Sep/23
In the case 1), [A] the 3−digit numbers span 100 to 999. [B] the numbers which are divisible by n appears every n positions. With these hints I presume you are smart enough to calculate the values you asked for.
$$ \\ $$$$\left.{In}\:{the}\:{case}\:\mathrm{1}\right),\: \\ $$$$\left[{A}\right]\:{the}\:\mathrm{3}−{digit}\:{numbers}\:{span} \\ $$$$\mathrm{100}\:{to}\:\mathrm{999}. \\ $$$$\left[{B}\right]\:{the}\:{numbers}\:{which}\:{are}\:{divisible} \\ $$$${by}\:\:\boldsymbol{\mathrm{n}}\:\:{appears}\:{every}\:\boldsymbol{\mathrm{n}}\:{positions}. \\ $$$$ \\ $$$${With}\:{these}\:{hints}\:{I}\:{presume}\:{you}\:{are} \\ $$$${smart}\:{enough}\:{to}\:{calculate}\:{the}\:{values} \\ $$$${you}\:{asked}\:{for}. \\ $$
Commented by mr W last updated on 24/Sep/23
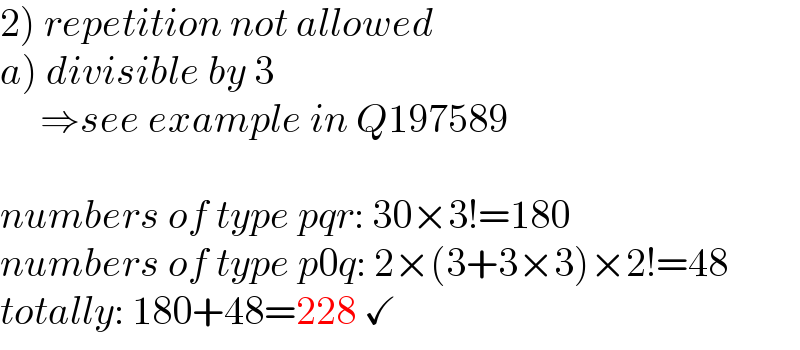
2) repetition not allowed a) divisible by 3 ⇒see example in Q197589 numbers of type pqr: 30×3!=180 numbers of type p0q: 2×(3+3×3)×2!=48 totally: 180+48=228 ✓
$$\left.\mathrm{2}\right)\:{repetition}\:{not}\:{allowed} \\ $$$$\left.{a}\right)\:{divisible}\:{by}\:\mathrm{3} \\ $$$$\:\:\:\:\:\Rightarrow{see}\:{example}\:{in}\:{Q}\mathrm{197589} \\ $$$$ \\ $$$${numbers}\:{of}\:{type}\:{pqr}:\:\mathrm{30}×\mathrm{3}!=\mathrm{180} \\ $$$${numbers}\:{of}\:{type}\:{p}\mathrm{0}{q}:\:\mathrm{2}×\left(\mathrm{3}+\mathrm{3}×\mathrm{3}\right)×\mathrm{2}!=\mathrm{48} \\ $$$${totally}:\:\mathrm{180}+\mathrm{48}=\mathrm{228}\:\checkmark\: \\ $$
Answered by Rasheed.Sindhi last updated on 22/Sep/23
(1)Repetition allowed_ If x is 3-digit number then 100≤x≤999 If x is 3-digit number divisible by d then ⌈((100)/d)⌉×d≤x≤⌊((999)/d)⌋×d and x is an AP with common difference d If a is first term a_n is last term(nth term) a_n =a+(n−1)d ⌊((999)/d)⌋×d=⌈((100)/d)⌉×d+(n−1)d ⌈((100)/d)⌉+(n−1)=⌊((999)/d)⌋ n=⌊((999)/d)⌋−⌈((100)/d)⌉+1 For example: (a) When d=3 n=⌊((999)/3)⌋−⌈((100)/3)⌉+1=333−34+1=300 So there are 300 3-digit numbers which are divisible by 3 (b) When d=4 n=⌊((999)/d)⌋−⌈((100)/d)⌉+1 =⌊((999)/4)⌋−⌈((100)/4)⌉+1=249−25+1=225 (c) When d=6 n=⌊((999)/d)⌋−⌈((100)/d)⌉+1 =⌊((999)/6)⌋−⌈((100)/6)⌉+1=166−17+1=150
$$\left(\mathrm{1}\right)\underline{{Repetition}\:{allowed}_{\:} } \\ $$$$\:{If}\:{x}\:{is}\:\mathrm{3}-{digit}\:{number}\:{then}\:\mathrm{100}\leqslant{x}\leqslant\mathrm{999} \\ $$$${If}\:{x}\:{is}\:\mathrm{3}-{digit}\:{number}\:{divisible}\:{by}\:{d}\:{then} \\ $$$$\lceil\frac{\mathrm{100}}{{d}}\rceil×{d}\leqslant{x}\leqslant\lfloor\frac{\mathrm{999}}{{d}}\rfloor×{d}\:{and}\:{x}\:{is}\:{an}\:{AP} \\ $$$${with}\:{common}\:{difference}\:{d} \\ $$$${If}\:{a}\:{is}\:{first}\:{term}\:{a}_{{n}} \:{is}\:{last}\:{term}\left({nth}\:{term}\right) \\ $$$${a}_{{n}} ={a}+\left({n}−\mathrm{1}\right){d} \\ $$$$\lfloor\frac{\mathrm{999}}{{d}}\rfloor×{d}=\lceil\frac{\mathrm{100}}{{d}}\rceil×{d}+\left({n}−\mathrm{1}\right){d} \\ $$$$\lceil\frac{\mathrm{100}}{{d}}\rceil+\left({n}−\mathrm{1}\right)=\lfloor\frac{\mathrm{999}}{{d}}\rfloor \\ $$$${n}=\lfloor\frac{\mathrm{999}}{{d}}\rfloor−\lceil\frac{\mathrm{100}}{{d}}\rceil+\mathrm{1} \\ $$$${For}\:{example}: \\ $$$$\left({a}\right)\:{When}\:{d}=\mathrm{3} \\ $$$${n}=\lfloor\frac{\mathrm{999}}{\mathrm{3}}\rfloor−\lceil\frac{\mathrm{100}}{\mathrm{3}}\rceil+\mathrm{1}=\mathrm{333}−\mathrm{34}+\mathrm{1}=\mathrm{300} \\ $$$${So}\:{there}\:{are}\:\mathrm{300}\:\:\:\mathrm{3}-{digit}\:{numbers}\:{which} \\ $$$${are}\:{divisible}\:{by}\:\mathrm{3} \\ $$$$\left({b}\right)\:{When}\:{d}=\mathrm{4} \\ $$$${n}=\lfloor\frac{\mathrm{999}}{{d}}\rfloor−\lceil\frac{\mathrm{100}}{{d}}\rceil+\mathrm{1} \\ $$$$\:\:=\lfloor\frac{\mathrm{999}}{\mathrm{4}}\rfloor−\lceil\frac{\mathrm{100}}{\mathrm{4}}\rceil+\mathrm{1}=\mathrm{249}−\mathrm{25}+\mathrm{1}=\mathrm{225} \\ $$$$\left({c}\right)\:{When}\:{d}=\mathrm{6} \\ $$$${n}=\lfloor\frac{\mathrm{999}}{{d}}\rfloor−\lceil\frac{\mathrm{100}}{{d}}\rceil+\mathrm{1} \\ $$$$\:\:=\lfloor\frac{\mathrm{999}}{\mathrm{6}}\rfloor−\lceil\frac{\mathrm{100}}{\mathrm{6}}\rceil+\mathrm{1}=\mathrm{166}−\mathrm{17}+\mathrm{1}=\mathrm{150} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *