Question-197834

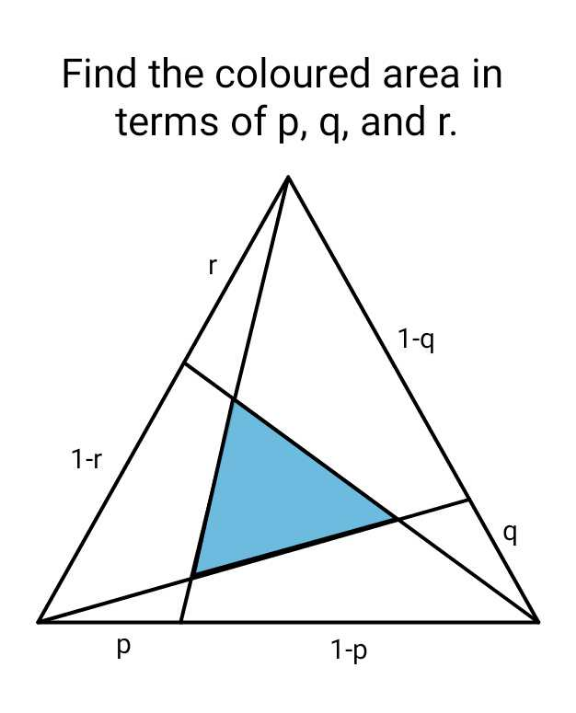
Question Number 197834 by ajfour last updated on 30/Sep/23

Answered by mr W last updated on 01/Oct/23

Commented by mr W last updated on 03/Oct/23

let Δ=area of ΔABC (any type triangle) ((HD)/(EC))=(p/1) ⇒HD=pqb ((GA)/(DG))=((AE)/(HD))=(((1−q)b)/(pqb))=(1/(pq))−(1/p) ((DG)/(DA))=((DG)/(DG+GA))=(1/(1+(1/(pq))−(1/p))) ((ΔBFG)/(ΔBDA))=((DG)/(DA))=(1/(1+(1/(pq))−(1/p))) ((ΔBDA)/Δ)=(p/1) ⇒ΔBDA=pΔ ⇒ΔBFG=((pΔ)/(1+(1/(pq))−(1/p))) similarly ⇒ΔCEK=((qΔ)/(1+(1/(qr))−(1/q))) ⇒ΔAFL=((rΔ)/(1+(1/(rp))−(1/r))) blue area+pΔ+qΔ+rΔ−2(((pΔ)/(1+(1/(pq))−(1/p)))+((qΔ)/(1+(1/(qr))−(1/q)))+((rΔ)/(1+(1/(rp))−(1/r))))=Δ ⇒((blue area)/Δ)=1+2((p/(1+(1/(pq))−(1/p)))+(q/(1+(1/(qr))−(1/q)))+(r/(1+(1/(rp))−(1/r))))−(p+q+r)

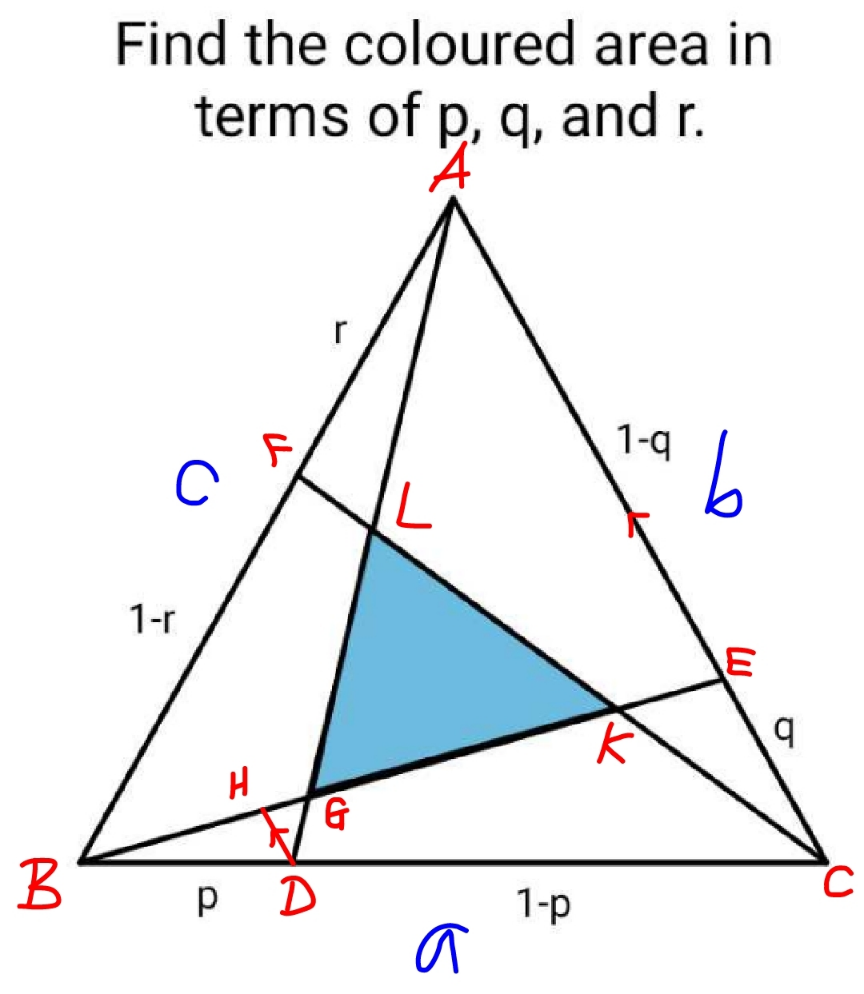
$${let}\:\Delta={area}\:{of}\:\Delta{ABC}\:\left({any}\:{type}\:{triangle}\right) \\ $$$$\frac{{HD}}{{EC}}=\frac{{p}}{\mathrm{1}} \\ $$$$\Rightarrow{HD}={pqb} \\ $$$$\frac{{GA}}{{DG}}=\frac{{AE}}{{HD}}=\frac{\left(\mathrm{1}−{q}\right){b}}{{pqb}}=\frac{\mathrm{1}}{{pq}}−\frac{\mathrm{1}}{{p}} \\ $$$$\frac{{DG}}{{DA}}=\frac{{DG}}{{DG}+{GA}}=\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{{pq}}−\frac{\mathrm{1}}{{p}}} \\ $$$$\frac{\Delta{BFG}}{\Delta{BDA}}=\frac{{DG}}{{DA}}=\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{{pq}}−\frac{\mathrm{1}}{{p}}} \\ $$$$\frac{\Delta{BDA}}{\Delta}=\frac{{p}}{\mathrm{1}} \\ $$$$\Rightarrow\Delta{BDA}={p}\Delta \\ $$$$\Rightarrow\Delta{BFG}=\frac{{p}\Delta}{\mathrm{1}+\frac{\mathrm{1}}{{pq}}−\frac{\mathrm{1}}{{p}}} \\ $$$${similarly} \\ $$$$\Rightarrow\Delta{CEK}=\frac{{q}\Delta}{\mathrm{1}+\frac{\mathrm{1}}{{qr}}−\frac{\mathrm{1}}{{q}}} \\ $$$$\Rightarrow\Delta{AFL}=\frac{{r}\Delta}{\mathrm{1}+\frac{\mathrm{1}}{{rp}}−\frac{\mathrm{1}}{{r}}} \\ $$$${blue}\:{area}+{p}\Delta+{q}\Delta+{r}\Delta−\mathrm{2}\left(\frac{{p}\Delta}{\mathrm{1}+\frac{\mathrm{1}}{{pq}}−\frac{\mathrm{1}}{{p}}}+\frac{{q}\Delta}{\mathrm{1}+\frac{\mathrm{1}}{{qr}}−\frac{\mathrm{1}}{{q}}}+\frac{{r}\Delta}{\mathrm{1}+\frac{\mathrm{1}}{{rp}}−\frac{\mathrm{1}}{{r}}}\right)=\Delta \\ $$$$\Rightarrow\frac{{blue}\:{area}}{\Delta}=\mathrm{1}+\mathrm{2}\left(\frac{{p}}{\mathrm{1}+\frac{\mathrm{1}}{{pq}}−\frac{\mathrm{1}}{{p}}}+\frac{{q}}{\mathrm{1}+\frac{\mathrm{1}}{{qr}}−\frac{\mathrm{1}}{{q}}}+\frac{{r}}{\mathrm{1}+\frac{\mathrm{1}}{{rp}}−\frac{\mathrm{1}}{{r}}}\right)−\left({p}+{q}+{r}\right) \\ $$

Answered by ajfour last updated on 01/Oct/23

Commented by ajfour last updated on 01/Oct/23

let △ABC has each side=2 with A origin O. B((√3),−1) C((√3),1) line PQ r_1 =λ[(√3)−i(1−q)] line QR r_2 =(√3)−i+μ[−(r/( (√3)))+i(2−(r/2))] line RP r_3 =(√3)+i+ε[−((√3)−(p/( (√3))))−i(1+(p/2))] P lies on r_1 & r_3 , hence (√3)λ=(√3)−ε((√3)−(p/( (√3)))) similarly λ(1−q)=−1+ε(1+(p/2)) ⇒ 1−ε(1−(p/3))(1−q)=−1+ε(1+(p/2)) ε[(1+(p/2))+(1−q)(1−(p/3))=2 λ=1−((2(1−(p/3)))/((1+(p/2))+(1−q)(1−(p/3)))) area △PQR=(1/2)PQ×PR (vector) ...pretty tedious this way Thank you sir.

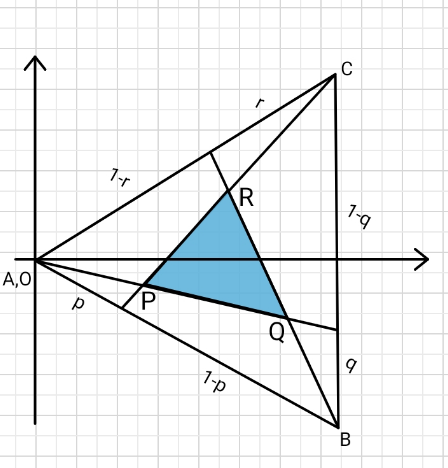
$${let}\:\bigtriangleup{ABC}\:{has}\:{each}\:{side}=\mathrm{2} \\ $$$${with}\:{A}\:{origin}\:{O}. \\ $$$${B}\left(\sqrt{\mathrm{3}},−\mathrm{1}\right)\:\:\:{C}\left(\sqrt{\mathrm{3}},\mathrm{1}\right) \\ $$$${line}\:\:{PQ} \\ $$$${r}_{\mathrm{1}} =\lambda\left[\sqrt{\mathrm{3}}−{i}\left(\mathrm{1}−{q}\right)\right] \\ $$$${line}\:{QR} \\ $$$${r}_{\mathrm{2}} =\sqrt{\mathrm{3}}−{i}+\mu\left[−\frac{{r}}{\:\sqrt{\mathrm{3}}}+{i}\left(\mathrm{2}−\frac{{r}}{\mathrm{2}}\right)\right] \\ $$$${line}\:{RP} \\ $$$${r}_{\mathrm{3}} =\sqrt{\mathrm{3}}+{i}+\epsilon\left[−\left(\sqrt{\mathrm{3}}−\frac{{p}}{\:\sqrt{\mathrm{3}}}\right)−{i}\left(\mathrm{1}+\frac{{p}}{\mathrm{2}}\right)\right] \\ $$$${P}\:\:{lies}\:{on}\:{r}_{\mathrm{1}} \&\:{r}_{\mathrm{3}} \:\:\:,\:{hence} \\ $$$$\sqrt{\mathrm{3}}\lambda=\sqrt{\mathrm{3}}−\epsilon\left(\sqrt{\mathrm{3}}−\frac{{p}}{\:\sqrt{\mathrm{3}}}\right) \\ $$$${similarly} \\ $$$$\lambda\left(\mathrm{1}−{q}\right)=−\mathrm{1}+\epsilon\left(\mathrm{1}+\frac{{p}}{\mathrm{2}}\right) \\ $$$$\Rightarrow\:\mathrm{1}−\epsilon\left(\mathrm{1}−\frac{{p}}{\mathrm{3}}\right)\left(\mathrm{1}−{q}\right)=−\mathrm{1}+\epsilon\left(\mathrm{1}+\frac{{p}}{\mathrm{2}}\right) \\ $$$$\epsilon\left[\left(\mathrm{1}+\frac{{p}}{\mathrm{2}}\right)+\left(\mathrm{1}−{q}\right)\left(\mathrm{1}−\frac{{p}}{\mathrm{3}}\right)=\mathrm{2}\right. \\ $$$$\lambda=\mathrm{1}−\frac{\mathrm{2}\left(\mathrm{1}−\frac{{p}}{\mathrm{3}}\right)}{\left(\mathrm{1}+\frac{{p}}{\mathrm{2}}\right)+\left(\mathrm{1}−{q}\right)\left(\mathrm{1}−\frac{{p}}{\mathrm{3}}\right)} \\ $$$${area}\:\bigtriangleup{PQR}=\frac{\mathrm{1}}{\mathrm{2}}{PQ}×{PR}\:\left({vector}\right) \\ $$$$…{pretty}\:{tedious}\:{this}\:{way} \\ $$$${Thank}\:{you}\:{sir}. \\ $$$$ \\ $$$$\:\: \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply