Question Number 197950 by York12 last updated on 05/Oct/23
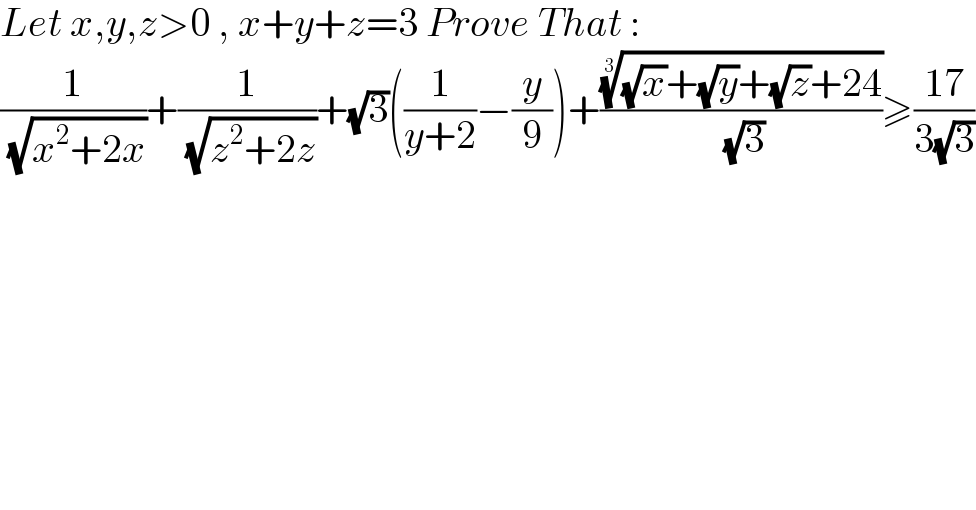
$${Let}\:{x},{y},{z}>\mathrm{0}\:,\:{x}+{y}+{z}=\mathrm{3}\:{Prove}\:{That}\:: \\ $$$$\frac{\mathrm{1}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{2}{x}}}+\frac{\mathrm{1}}{\:\sqrt{{z}^{\mathrm{2}} +\mathrm{2}{z}}}+\sqrt{\mathrm{3}}\left(\frac{\mathrm{1}}{{y}+\mathrm{2}}−\frac{{y}}{\mathrm{9}}\right)+\frac{\sqrt[{\mathrm{3}}]{\sqrt{{x}}+\sqrt{{y}}+\sqrt{{z}}+\mathrm{24}}}{\:\sqrt{\mathrm{3}}}\geqslant\frac{\mathrm{17}}{\mathrm{3}\sqrt{\mathrm{3}}} \\ $$
