Question Number 197980 by mr W last updated on 07/Oct/23
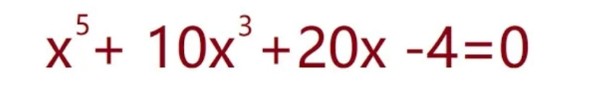
Commented by mr W last updated on 07/Oct/23

$${please}\:{exact}\:{solution}! \\ $$
Commented by Blackpanther last updated on 07/Oct/23
0.196....only real solution
Commented by Frix last updated on 07/Oct/23

$$\mathrm{After}\:\mathrm{trying}\:\mathrm{for}\:\mathrm{a}\:\mathrm{while}: \\ $$$${x}=\mathrm{2}^{\frac{\mathrm{3}}{\mathrm{5}}} −\mathrm{2}^{\frac{\mathrm{2}}{\mathrm{5}}} \\ $$$$\mathrm{Not}\:\mathrm{sure}\:\mathrm{how}\:\mathrm{to}\:\mathrm{get}\:\mathrm{it}\:\mathrm{analytically} \\ $$
Commented by mr W last updated on 07/Oct/23
��
Answered by mr W last updated on 07/Oct/23

$${for}\:{this}\:{kind}\:{of}\:{quintic}\:{equations} \\ $$$${we}\:{can}\:{try}\:{with}\:{a}\:{substitution}\:{like} \\ $$$${x}={t}+\frac{{a}}{{t}},\:{here}\:{with}\:{x}={t}−\frac{\mathrm{2}}{{t}}.\:{then} \\ $$$${we}\:{get} \\ $$$${t}^{\mathrm{5}} −\frac{\mathrm{32}}{{t}^{\mathrm{5}} }−\mathrm{4}=\mathrm{0},\:{or} \\ $$$${t}^{\mathrm{10}} −\mathrm{4}{t}^{\mathrm{5}} −\mathrm{32}=\mathrm{0} \\ $$$$\left({t}^{\mathrm{5}} −\mathrm{8}\right)\left({t}^{\mathrm{5}} +\mathrm{4}\right)=\mathrm{0} \\ $$$$\Rightarrow{t}^{\mathrm{5}} =\mathrm{8}\:\Rightarrow{t}=\sqrt[{\mathrm{5}}]{\mathrm{8}} \\ $$$$\Rightarrow{x}=\sqrt[{\mathrm{5}}]{\mathrm{8}}−\frac{\mathrm{2}}{\:\sqrt[{\mathrm{5}}]{\mathrm{8}}}=\mathrm{2}^{\frac{\mathrm{3}}{\mathrm{5}}} −\mathrm{2}^{\frac{\mathrm{2}}{\mathrm{5}}} \approx\mathrm{0}.\mathrm{196209} \\ $$
Commented by mr W last updated on 07/Oct/23

$${it}\:{can}\:{be}\:{easily}\:{checked}\:{that}\:{the}\:{eqn}. \\ $$$${has}\:{one}\:{and}\:{only}\:{one}\:{real}\:{root}\: \\ $$$${between}\:\mathrm{0}\:{and}\:\mathrm{1}. \\ $$$${f}\left(\mathrm{0}\right)=−\mathrm{4}<\mathrm{0} \\ $$$${f}\left(\mathrm{1}\right)=\mathrm{27}>\mathrm{0} \\ $$$${f}'\left({x}\right)=\mathrm{5}{x}^{\mathrm{4}} +\mathrm{30}{x}^{\mathrm{2}} +\mathrm{20}>\mathrm{0} \\ $$
Commented by mr W last updated on 07/Oct/23

$${yes}.\:{only}\:{solvable}\:{if}\:{p}^{\mathrm{2}} =\mathrm{5}{q}. \\ $$
Commented by Frix last updated on 07/Oct/23

$$\mathrm{But}\:\mathrm{this}\:\mathrm{is}\:\mathrm{only}\:\mathrm{good}\:\mathrm{luck}. \\ $$$${x}^{\mathrm{5}} +{px}^{\mathrm{3}} +{qx}+{r}=\mathrm{0} \\ $$$${x}={t}+\frac{{a}}{{t}}\:\Rightarrow \\ $$$${t}^{\mathrm{5}} +\left(\mathrm{5}{a}+{p}\right){t}^{\mathrm{3}} +\left(\mathrm{10}{a}^{\mathrm{2}} +\mathrm{3}{ap}+{q}\right){t}+\frac{{a}\left(\mathrm{10}{a}^{\mathrm{2}} +\mathrm{3}{ap}+{q}\right)}{{t}}+\frac{{a}^{\mathrm{3}} \left(\mathrm{5}{a}+{p}\right)}{{t}^{\mathrm{3}} }+\frac{{a}^{\mathrm{5}} }{{t}^{\mathrm{5}} }+{r}=\mathrm{0} \\ $$$$\mathrm{It}\:\mathrm{works}\:\mathrm{only}\:\mathrm{if} \\ $$$${q}=\frac{{p}^{\mathrm{2}} }{\mathrm{5}}\:\Rightarrow\:{a}=−\frac{{p}}{\mathrm{5}}=\pm\frac{\sqrt{\mathrm{5}{q}}}{\mathrm{5}} \\ $$$$\Rightarrow \\ $$$${t}^{\mathrm{5}} +\frac{{a}^{\mathrm{5}} }{{t}^{\mathrm{5}} }+{r}=\mathrm{0} \\ $$
Answered by a.lgnaoui last updated on 07/Oct/23
![x(x^4 +10x^2 +20)=4 x((x+5)^2 −5]=4 [(x+5)−5)][(x+5)^2 −5]=4 x+5=z (z−5)(z^2 −5)=4 z^3 −5z−5z^2 +21=0 after reolving the equagion we get z={−2,206449 1,9234927 5,182957} x=z−5 { ((x_1 =−3,0765 x_2 = 0,182957)),(( x_3 =−7,10644)) :}](https://www.tinkutara.com/question/Q198002.png)
$$\:\:\:\boldsymbol{\mathrm{x}}\left(\boldsymbol{\mathrm{x}}^{\mathrm{4}} +\mathrm{10}\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{20}\right)=\mathrm{4} \\ $$$$\:\:\boldsymbol{\mathrm{x}}\left(\left(\boldsymbol{\mathrm{x}}+\mathrm{5}\right)^{\mathrm{2}} −\mathrm{5}\right]=\mathrm{4} \\ $$$$\left.\:\:\:\:\left[\left(\boldsymbol{\mathrm{x}}+\mathrm{5}\right)−\mathrm{5}\right)\right]\left[\left(\boldsymbol{\mathrm{x}}+\mathrm{5}\right)^{\mathrm{2}} −\mathrm{5}\right]=\mathrm{4} \\ $$$$\:\:\:\:\:\boldsymbol{\mathrm{x}}+\mathrm{5}=\boldsymbol{\mathrm{z}} \\ $$$$\:\:\:\:\:\left(\boldsymbol{\mathrm{z}}−\mathrm{5}\right)\left(\boldsymbol{\mathrm{z}}^{\mathrm{2}} −\mathrm{5}\right)=\mathrm{4} \\ $$$$\:\:\:\:\boldsymbol{\mathrm{z}}^{\mathrm{3}} −\mathrm{5}\boldsymbol{\mathrm{z}}−\mathrm{5}\boldsymbol{\mathrm{z}}^{\mathrm{2}} +\mathrm{21}=\mathrm{0} \\ $$$$\:\:\:\:\mathrm{after}\:\mathrm{reolving}\:\mathrm{the}\:\mathrm{equagion}\:\mathrm{we}\:\:\:\mathrm{get} \\ $$$$\:\:\:\:\:\mathrm{z}=\left\{−\mathrm{2},\mathrm{206449}\:\:\:\mathrm{1},\mathrm{9234927}\:\:\:\:\mathrm{5},\mathrm{182957}\right\} \\ $$$$\:\:\:\:\:\boldsymbol{\mathrm{x}}=\boldsymbol{\mathrm{z}}−\mathrm{5} \\ $$$$ \\ $$$$\begin{cases}{\mathrm{x}_{\mathrm{1}} =−\mathrm{3},\mathrm{0765}\:\:\:\:\:\:\boldsymbol{\mathrm{x}}_{\mathrm{2}} \:=\:\mathrm{0},\mathrm{182957}}\\{\:\boldsymbol{\mathrm{x}}_{\mathrm{3}} =−\mathrm{7},\mathrm{10644}}\end{cases} \\ $$
Commented by Frix last updated on 07/Oct/23

$${x}\left({x}^{\mathrm{4}} +\mathrm{10}{x}^{\mathrm{2}} +\mathrm{20}\right)=\mathrm{4}\:\Rightarrow\:{x}\left(\left({x}^{\mathrm{2}} +\mathrm{5}\right)^{\mathrm{2}} −\mathrm{5}\right)=\mathrm{4} \\ $$
Commented by a.lgnaoui last updated on 07/Oct/23
![oh yes thanks so we must changed z by x+5 and cintunue[to resultst]](https://www.tinkutara.com/question/Q198004.png)
$$\mathrm{oh}\:\:\mathrm{yes}\:\:\mathrm{thanks} \\ $$$$\mathrm{so}\:\:\:\mathrm{we}\:\mathrm{must}\:\mathrm{changed}\:\mathrm{z}\:\:\mathrm{by}\:\boldsymbol{\mathrm{x}}+\mathrm{5} \\ $$$$\mathrm{and}\:\:\mathrm{cintunue}\left[\mathrm{to}\:\mathrm{resultst}\right] \\ $$
Commented by a.lgnaoui last updated on 07/Oct/23
^2 −5]=4 (z−5)(z^2 −5)=4 z^3 −5z^2 −5z+21=0 ⇒ x={−3,0765, 0,182957 , − 7,106449 }](https://www.tinkutara.com/question/Q198005.png)
$$\left.\left[\left(\mathrm{x}+\mathrm{5}\right)−\mathrm{5}\right]\left(\mathrm{x}+\mathrm{5}\right)^{\mathrm{2}} −\mathrm{5}\right]=\mathrm{4} \\ $$$$\left(\mathrm{z}−\mathrm{5}\right)\left(\mathrm{z}^{\mathrm{2}} −\mathrm{5}\right)=\mathrm{4} \\ $$$$\:\:\mathrm{z}^{\mathrm{3}} −\mathrm{5z}^{\mathrm{2}} −\mathrm{5z}+\mathrm{21}=\mathrm{0} \\ $$$$\Rightarrow\:\:\:\boldsymbol{\mathrm{x}}=\left\{−\mathrm{3},\mathrm{0765},\:\:\:\mathrm{0},\mathrm{182957}\:,\:−\:\mathrm{7},\mathrm{106449}\:\right\} \\ $$
Commented by Frix last updated on 07/Oct/23

$$\mathrm{It}'\mathrm{s}\:\mathrm{still}\:\mathrm{wrong}.\:\mathrm{You}\:\mathrm{used}\:{x}\left(\left({x}+\mathrm{5}\right)^{\mathrm{2}} −\mathrm{5}\right)=\mathrm{4} \\ $$$$\mathrm{instead}\:\mathrm{of}\:{x}\left(\left({x}^{\mathrm{2}} +\mathrm{5}\right)^{\mathrm{2}} −\mathrm{5}\right)=\mathrm{4} \\ $$
