Question Number 198178 by universe last updated on 13/Oct/23
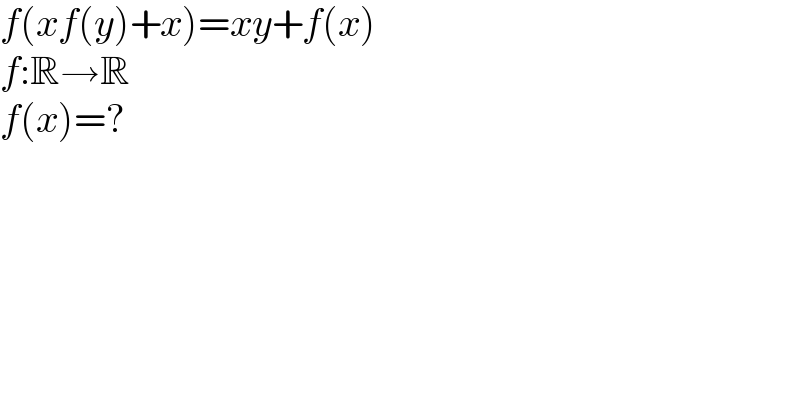
$${f}\left({xf}\left({y}\right)+{x}\right)={xy}+{f}\left({x}\right) \\ $$$${f}:\mathbb{R}\rightarrow\mathbb{R} \\ $$$${f}\left({x}\right)=? \\ $$
Answered by Rasheed.Sindhi last updated on 13/Oct/23

$${Let}\:{f}\left({x}\right)={ax}+{b} \\ $$$${f}\left({xf}\left({y}\right)+{x}\right)={xy}+{f}\left({x}\right) \\ $$$$\Rightarrow{a}\left({xf}\left({y}\right)+{x}\right)+{b}={xy}+{ax}+{b} \\ $$$$\Rightarrow{ax}\left({ay}+{b}\right)+{ax}={xy}+{ax} \\ $$$$\Rightarrow{ax}\left({ay}+{b}\right)={xy} \\ $$$${y}\rightarrow{x} \\ $$$$\Rightarrow{ax}\left({ax}+{b}\right)={x}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:{a}^{\mathrm{2}} {x}^{\mathrm{2}} +{bx}={x}^{\mathrm{2}} \\ $$$$\:\:\:\:{a}^{\mathrm{2}} =\mathrm{1}\wedge\:{b}=\mathrm{0} \\ $$$$\:\:\:\:\:{a}=\pm\mathrm{1}\:\wedge\:{b}=\mathrm{0} \\ $$$${f}\left({x}\right)={ax}+{b}=\left(\pm\mathrm{1}\right){x}+\mathrm{0} \\ $$$$\begin{array}{|c|}{\begin{array}{|c|}{{f}\left({x}\right)={x}\:\:\:\mid\:\:\:{f}\left({x}\right)=−{x}}\\\hline\end{array}}\\\hline\end{array} \\ $$$${Verification}: \\ $$$$\left(\mathrm{1}\right)\:{f}\left({x}\right)={x} \\ $$$${f}\left({xf}\left({y}\right)+{x}\right)={xy}+{f}\left({x}\right) \\ $$$${xf}\left({y}\right)+{x}={xy}+{f}\left({x}\right) \\ $$$$\Rightarrow{xy}+{x}={xy}+{x}\:\left(\checkmark\right) \\ $$$$\left(\mathrm{2}\right)\:{f}\left({x}\right)=−{x} \\ $$$${f}\left({xf}\left({y}\right)+{x}\right)={xy}+{f}\left({x}\right) \\ $$$$\Rightarrow−{xf}\left({y}\right)−{x}={xy}−{x} \\ $$$$\Rightarrow−{xf}\left({y}\right)−{x}={xy}−{x} \\ $$$$\Rightarrow−{x}\left(−{y}\right)−{x}={xy}−{x} \\ $$$$\Rightarrow{xy}−{x}={xy}−{x}\:\left(\checkmark\right) \\ $$
Commented by mr W last updated on 13/Oct/23
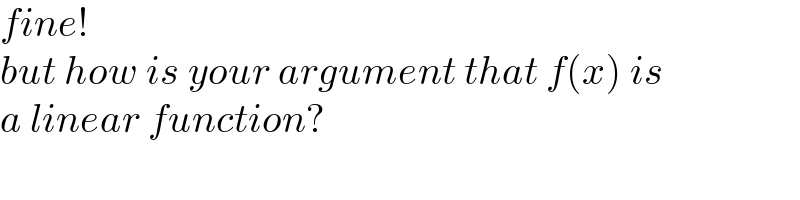
$${fine}! \\ $$$${but}\:{how}\:{is}\:{your}\:{argument}\:{that}\:{f}\left({x}\right)\:{is} \\ $$$${a}\:{linear}\:{function}? \\ $$
Commented by Rasheed.Sindhi last updated on 13/Oct/23

$$\boldsymbol{{sir}},\:{I}'{ve}\:{no}\:{argument}!\:{Even}\:{about}\:\: \\ $$$$\:{the}\:{function}\:{to}\:{be}\:{polynomial}!\:{But}\:{there}'{s} \\ $$$$\:{possibility}\:{of}\:{being}\:{linear}. \\ $$
Answered by witcher3 last updated on 13/Oct/23
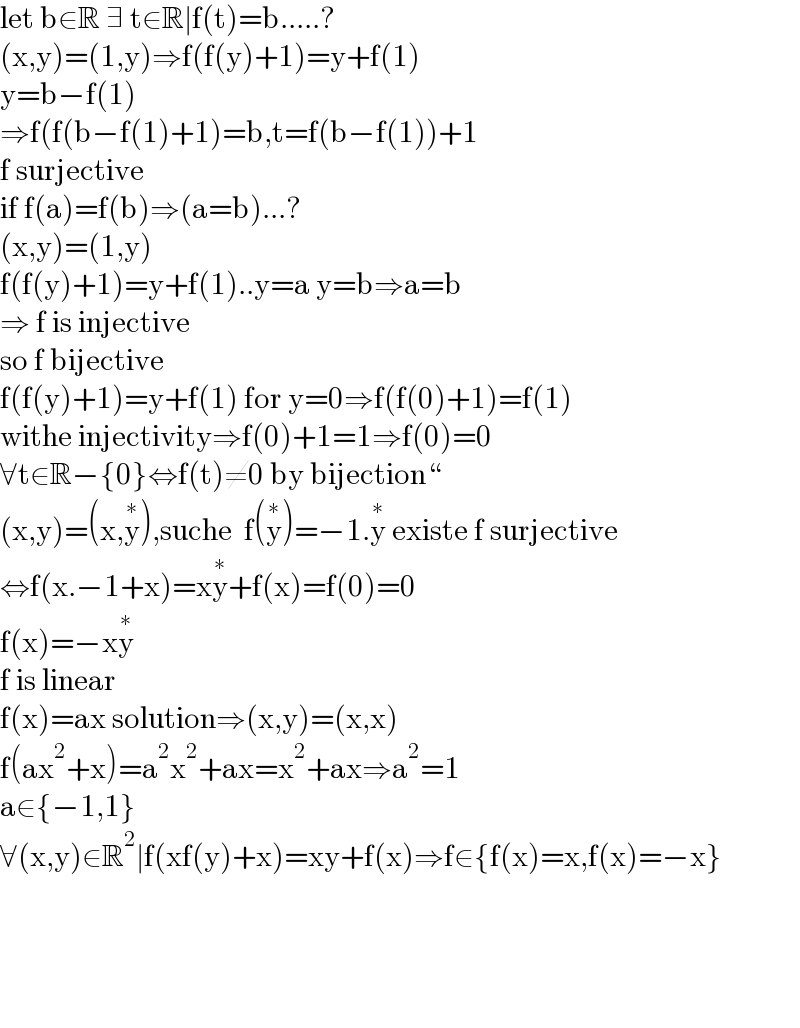
$$\mathrm{let}\:\mathrm{b}\in\mathbb{R}\:\exists\:\mathrm{t}\in\mathbb{R}\mid\mathrm{f}\left(\mathrm{t}\right)=\mathrm{b}…..? \\ $$$$\left(\mathrm{x},\mathrm{y}\right)=\left(\mathrm{1},\mathrm{y}\right)\Rightarrow\mathrm{f}\left(\mathrm{f}\left(\mathrm{y}\right)+\mathrm{1}\right)=\mathrm{y}+\mathrm{f}\left(\mathrm{1}\right) \\ $$$$\mathrm{y}=\mathrm{b}−\mathrm{f}\left(\mathrm{1}\right) \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{f}\left(\mathrm{b}−\mathrm{f}\left(\mathrm{1}\right)+\mathrm{1}\right)=\mathrm{b},\mathrm{t}=\mathrm{f}\left(\mathrm{b}−\mathrm{f}\left(\mathrm{1}\right)\right)+\mathrm{1}\right. \\ $$$$\mathrm{f}\:\mathrm{surjective} \\ $$$$\mathrm{if}\:\mathrm{f}\left(\mathrm{a}\right)=\mathrm{f}\left(\mathrm{b}\right)\Rightarrow\left(\mathrm{a}=\mathrm{b}\right)…? \\ $$$$\left(\mathrm{x},\mathrm{y}\right)=\left(\mathrm{1},\mathrm{y}\right) \\ $$$$\mathrm{f}\left(\mathrm{f}\left(\mathrm{y}\right)+\mathrm{1}\right)=\mathrm{y}+\mathrm{f}\left(\mathrm{1}\right)..\mathrm{y}=\mathrm{a}\:\mathrm{y}=\mathrm{b}\Rightarrow\mathrm{a}=\mathrm{b} \\ $$$$\Rightarrow\:\mathrm{f}\:\mathrm{is}\:\mathrm{injective}\:\: \\ $$$$\mathrm{so}\:\mathrm{f}\:\mathrm{bijective} \\ $$$$\mathrm{f}\left(\mathrm{f}\left(\mathrm{y}\right)+\mathrm{1}\right)=\mathrm{y}+\mathrm{f}\left(\mathrm{1}\right)\:\mathrm{for}\:\mathrm{y}=\mathrm{0}\Rightarrow\mathrm{f}\left(\mathrm{f}\left(\mathrm{0}\right)+\mathrm{1}\right)=\mathrm{f}\left(\mathrm{1}\right) \\ $$$$\mathrm{withe}\:\mathrm{injectivity}\Rightarrow\mathrm{f}\left(\mathrm{0}\right)+\mathrm{1}=\mathrm{1}\Rightarrow\mathrm{f}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$$\forall\mathrm{t}\in\mathbb{R}−\left\{\mathrm{0}\right\}\Leftrightarrow\mathrm{f}\left(\mathrm{t}\right)\neq\mathrm{0}\:\mathrm{by}\:\mathrm{bijection}“ \\ $$$$\left(\mathrm{x},\mathrm{y}\right)=\left(\mathrm{x},\overset{\ast} {\mathrm{y}}\right),\mathrm{suche}\:\:\mathrm{f}\left(\overset{\ast} {\mathrm{y}}\right)=−\mathrm{1}.\overset{\ast} {\mathrm{y}}\:\mathrm{existe}\:\mathrm{f}\:\mathrm{surjective} \\ $$$$\Leftrightarrow\mathrm{f}\left(\mathrm{x}.−\mathrm{1}+\mathrm{x}\right)=\mathrm{x}\overset{\ast} {\mathrm{y}}+\mathrm{f}\left(\mathrm{x}\right)=\mathrm{f}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=−\mathrm{x}\overset{\ast} {\mathrm{y}} \\ $$$$\mathrm{f}\:\mathrm{is}\:\mathrm{linear}\:\: \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{ax}\:\mathrm{solution}\Rightarrow\left(\mathrm{x},\mathrm{y}\right)=\left(\mathrm{x},\mathrm{x}\right) \\ $$$$\mathrm{f}\left(\mathrm{ax}^{\mathrm{2}} +\mathrm{x}\right)=\mathrm{a}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} +\mathrm{ax}=\mathrm{x}^{\mathrm{2}} +\mathrm{ax}\Rightarrow\mathrm{a}^{\mathrm{2}} =\mathrm{1} \\ $$$$\mathrm{a}\in\left\{−\mathrm{1},\mathrm{1}\right\} \\ $$$$\forall\left(\mathrm{x},\mathrm{y}\right)\in\mathbb{R}^{\mathrm{2}} \mid\mathrm{f}\left(\mathrm{xf}\left(\mathrm{y}\right)+\mathrm{x}\right)=\mathrm{xy}+\mathrm{f}\left(\mathrm{x}\right)\Rightarrow\mathrm{f}\in\left\{\mathrm{f}\left(\mathrm{x}\right)=\mathrm{x},\mathrm{f}\left(\mathrm{x}\right)=−\mathrm{x}\right\} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
