Question-198231

Question Number 198231 by pticantor last updated on 14/Oct/23

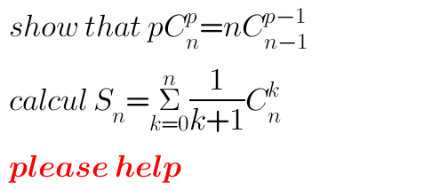
Answered by witcher3 last updated on 14/Oct/23

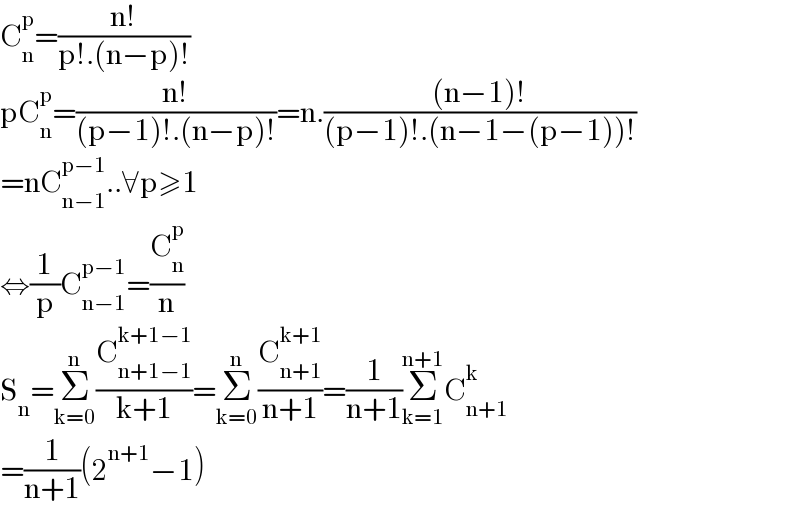
C_n ^p =((n!)/(p!.(n−p)!)) pC_n ^p =((n!)/((p−1)!.(n−p)!))=n.(((n−1)!)/((p−1)!.(n−1−(p−1))!)) =nC_(n−1) ^(p−1) ..∀p≥1 ⇔(1/p)C_(n−1) ^(p−1) =(C_n ^p /n) S_n =Σ_(k=0) ^n (C_(n+1−1) ^(k+1−1) /(k+1))=Σ_(k=0) ^n (C_(n+1) ^(k+1) /(n+1))=(1/(n+1))Σ_(k=1) ^(n+1) C_(n+1) ^k =(1/(n+1))(2^(n+1) −1)

$$\mathrm{C}_{\mathrm{n}} ^{\mathrm{p}} =\frac{\mathrm{n}!}{\mathrm{p}!.\left(\mathrm{n}−\mathrm{p}\right)!} \\ $$$$\mathrm{pC}_{\mathrm{n}} ^{\mathrm{p}} =\frac{\mathrm{n}!}{\left(\mathrm{p}−\mathrm{1}\right)!.\left(\mathrm{n}−\mathrm{p}\right)!}=\mathrm{n}.\frac{\left(\mathrm{n}−\mathrm{1}\right)!}{\left(\mathrm{p}−\mathrm{1}\right)!.\left(\mathrm{n}−\mathrm{1}−\left(\mathrm{p}−\mathrm{1}\right)\right)!} \\ $$$$=\mathrm{nC}_{\mathrm{n}−\mathrm{1}} ^{\mathrm{p}−\mathrm{1}} ..\forall\mathrm{p}\geqslant\mathrm{1} \\ $$$$\Leftrightarrow\frac{\mathrm{1}}{\mathrm{p}}\mathrm{C}_{\mathrm{n}−\mathrm{1}} ^{\mathrm{p}−\mathrm{1}} =\frac{\mathrm{C}_{\mathrm{n}} ^{\mathrm{p}} }{\mathrm{n}} \\ $$$$\mathrm{S}_{\mathrm{n}} =\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{C}_{\mathrm{n}+\mathrm{1}−\mathrm{1}} ^{\mathrm{k}+\mathrm{1}−\mathrm{1}} }{\mathrm{k}+\mathrm{1}}=\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{C}_{\mathrm{n}+\mathrm{1}} ^{\mathrm{k}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}+\mathrm{1}} {\sum}}\mathrm{C}_{\mathrm{n}+\mathrm{1}} ^{\mathrm{k}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}\left(\mathrm{2}^{\mathrm{n}+\mathrm{1}} −\mathrm{1}\right) \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply