You-want-to-arrange-17-books-on-the-shelf-of-a-bookstore-The-shelf-is-dedicated-to-the-three-Toni-Morrison-novels-published-between-1977-and-1987-Song-of-Solomon-Tar-Baby-and-Beloved-You-have-man

Question Number 198851 by Tawa11 last updated on 25/Oct/23

You want to arrange 17 books on the shelf of a bookstore.
The shelf is dedicated to the three Toni Morrison novels
published between 1977 and 1987: Song of Solomon,
Tar Baby, and Beloved. You have many copies of each,
but on the shelf you want an even number of Song of
Solomon, at least three copies of Tar Baby, and at most
four copies of Beloved. How many different arrangements
are possible?

Commented by mr W last updated on 25/Oct/23

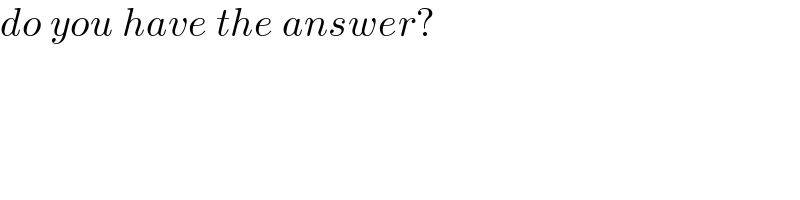
$${do}\:{you}\:{have}\:{the}\:{answer}? \\ $$

Commented by mr W last updated on 25/Oct/23

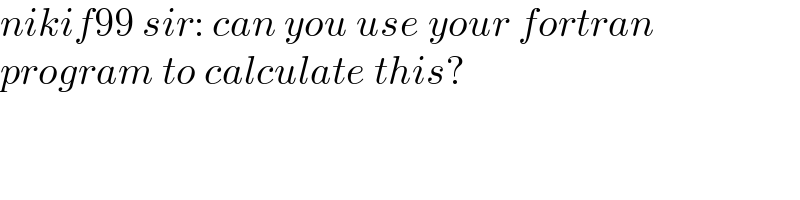
nikif99 sir: can you use your fortran program to calculate this?

$${nikif}\mathrm{99}\:{sir}:\:{can}\:{you}\:{use}\:{your}\:{fortran} \\ $$$${program}\:{to}\:{calculate}\:{this}? \\ $$

Commented by Tawa11 last updated on 25/Oct/23

$$\mathrm{yes}\:\mathrm{sir} \\ $$

Commented by mr W last updated on 25/Oct/23

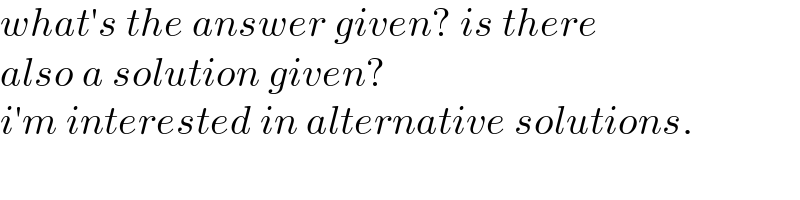
$${what}'{s}\:{the}\:{answer}\:{given}?\:{is}\:{there} \\ $$$${also}\:{a}\:{solution}\:{given}? \\ $$$${i}'{m}\:{interested}\:{in}\:{alternative}\:{solutions}. \\ $$

Commented by Tawa11 last updated on 25/Oct/23

$$\mathrm{18},\mathrm{072},\mathrm{242} \\ $$

Commented by Tawa11 last updated on 25/Oct/23

$$\mathrm{yes}\:\mathrm{sir} \\ $$

Commented by Tawa11 last updated on 25/Oct/23

$$\mathrm{Should}\:\mathrm{I}\:\mathrm{send}\:\mathrm{the}\:\mathrm{solution}\:\mathrm{now}\:\mathrm{sir}? \\ $$

Commented by nikif99 last updated on 25/Oct/23

if 0 books are allowed for “Song of Solomon” or “Beloved” I found 18.072.242 cases. If not, then cases are limited to 18.003.510. Left 3 columns are possible number of copies selected of three titles, when 0 books are allowed. Right 3 columns excempt 0 books. For each horizontal line, number of arrangements with repetitions is ((17!)/(a!×b!×c!))

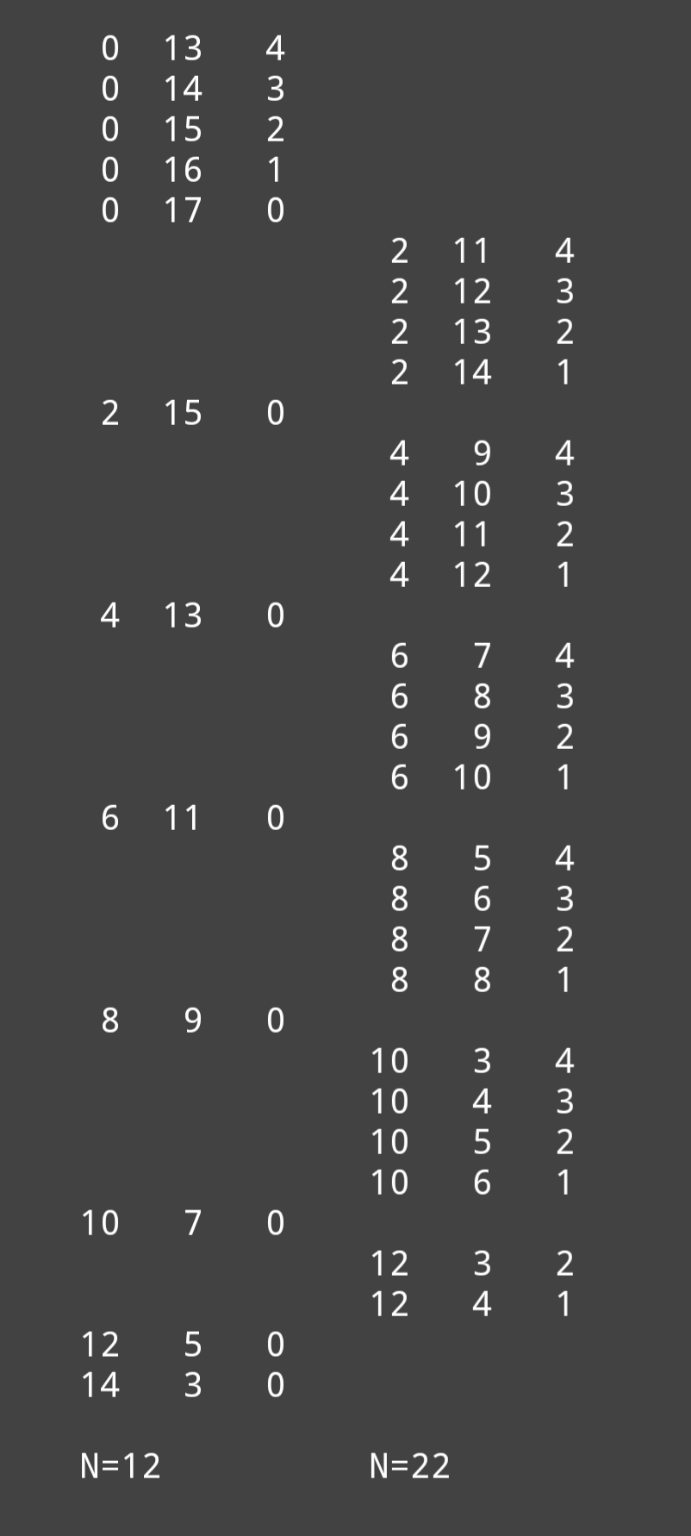
$${if}\:\mathrm{0}\:{books}\:{are}\:{allowed}\:{for}\:“{Song}\:{of}\: \\ $$$${Solomon}''\:{or}\:“{Beloved}''\:{I}\:{found} \\ $$$$\mathrm{18}.\mathrm{072}.\mathrm{242}\:{cases}. \\ $$$${If}\:{not},\:{then}\:{cases}\:{are}\:{limited}\:{to} \\ $$$$\mathrm{18}.\mathrm{003}.\mathrm{510}. \\ $$$${Left}\:\mathrm{3}\:{columns}\:{are}\:{possible}\:{number}\:{of} \\ $$$${copies}\:{selected}\:{of}\:{three}\:{titles},\:{when} \\ $$$$\mathrm{0}\:{books}\:{are}\:{allowed}. \\ $$$${Right}\:\mathrm{3}\:{columns}\:{excempt}\:\mathrm{0}\:{books}. \\ $$$${For}\:{each}\:{horizontal}\:{line},\:{number}\:{of} \\ $$$${arrangements}\:{with}\:{repetitions}\:{is} \\ $$$$\frac{\mathrm{17}!}{{a}!×{b}!×{c}!} \\ $$$$ \\ $$

Commented by nikif99 last updated on 25/Oct/23

Commented by Tawa11 last updated on 25/Oct/23

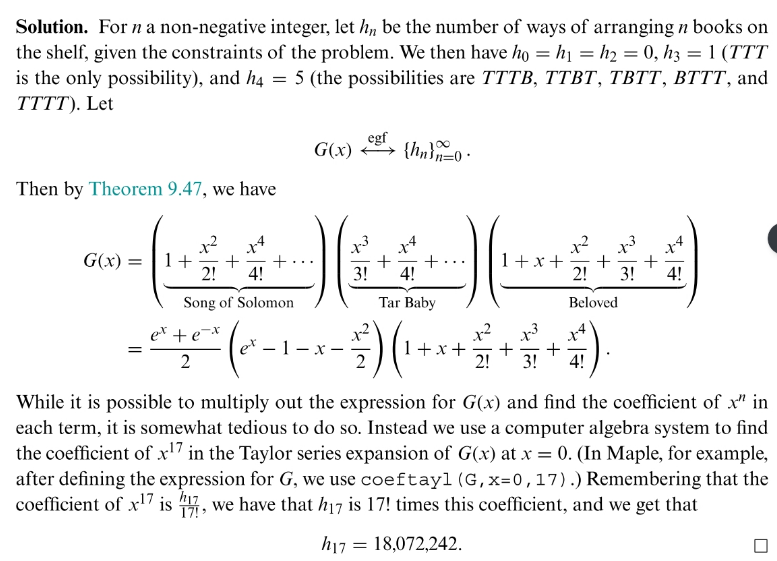
Commented by mr W last updated on 25/Oct/23

$${are}\:{you}\:{also}\:{familiar}\:{with}\:{generating} \\ $$$${functions}? \\ $$

Commented by Tawa11 last updated on 25/Oct/23

No sir. I saw the method in your previous solution so, I bring the question here.

$$\mathrm{No}\:\mathrm{sir}. \\ $$$$\mathrm{I}\:\mathrm{saw}\:\mathrm{the}\:\mathrm{method}\:\mathrm{in}\:\mathrm{your}\:\mathrm{previous}\:\mathrm{solution}\:\mathrm{so}, \\ $$$$\mathrm{I}\:\mathrm{bring}\:\mathrm{the}\:\mathrm{question}\:\mathrm{here}. \\ $$

Answered by mr W last updated on 26/Oct/23

once again i′ll try to use generating functions. s=number of books “Song of Solomon” t=number of books “Tar Baby” b=number of books “Beloved” s⇒(x^2 +x^4 +x^6 +...) t⇒(x^3 +x^4 +x^5 +...) b⇒(x+x^2 +x^3 +x^4 ) s+t+b=17 number of arrangements is the coefficient of x^(17) term in expansion 17!((x^2 /(2!))+(x^4 /(4!))+(x^6 /(6!))+...)((x^3 /(3!))+(x^4 /(4!))+(x^5 /(5!))+...)(x+(x^2 /(2!))+(x^3 /(3!))+(x^4 /(4!))) which is 18 003 510. if no book from S anf B is also allowed, then the answer is the coefficient of x^(17) term in 17!(1+(x^2 /(2!))+(x^4 /(4!))+(x^6 /(6!))+...)((x^3 /(3!))+(x^4 /(4!))+(x^5 /(5!))+...)(1+x+(x^2 /(2!))+(x^3 /(3!))+(x^4 /(4!))) which is 18 072 242.

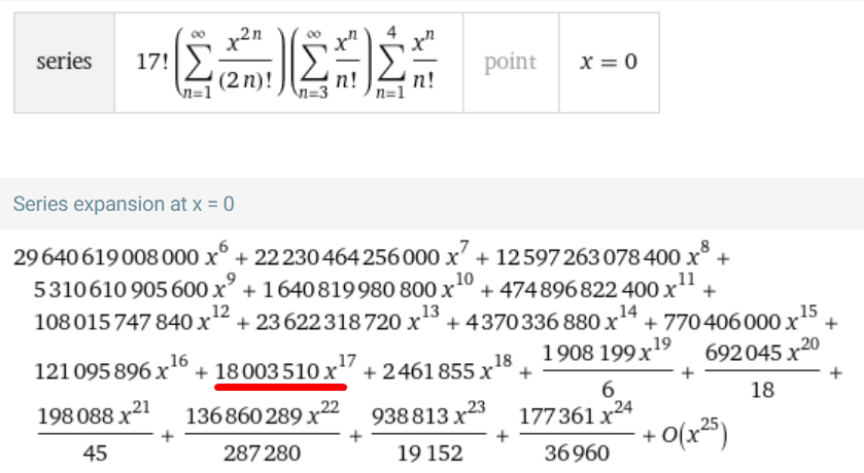
$${once}\:{again}\:{i}'{ll}\:{try}\:{to}\:{use}\:{generating} \\ $$$${functions}. \\ $$$${s}={number}\:{of}\:{books}\:“{Song}\:{of}\:{Solomon}'' \\ $$$${t}={number}\:{of}\:{books}\:“{Tar}\:{Baby}'' \\ $$$${b}={number}\:{of}\:{books}\:“{Beloved}'' \\ $$$${s}\Rightarrow\left({x}^{\mathrm{2}} +{x}^{\mathrm{4}} +{x}^{\mathrm{6}} +…\right) \\ $$$${t}\Rightarrow\left({x}^{\mathrm{3}} +{x}^{\mathrm{4}} +{x}^{\mathrm{5}} +…\right) \\ $$$${b}\Rightarrow\left({x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +{x}^{\mathrm{4}} \right) \\ $$$${s}+{t}+{b}=\mathrm{17} \\ $$$${number}\:{of}\:{arrangements}\:{is}\:{the} \\ $$$${coefficient}\:{of}\:{x}^{\mathrm{17}} \:{term}\:{in}\:{expansion} \\ $$$$\mathrm{17}!\left(\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}+\frac{{x}^{\mathrm{4}} }{\mathrm{4}!}+\frac{{x}^{\mathrm{6}} }{\mathrm{6}!}+…\right)\left(\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}+\frac{{x}^{\mathrm{4}} }{\mathrm{4}!}+\frac{{x}^{\mathrm{5}} }{\mathrm{5}!}+…\right)\left({x}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}+\frac{{x}^{\mathrm{4}} }{\mathrm{4}!}\right) \\ $$$${which}\:{is}\:\mathrm{18}\:\mathrm{003}\:\mathrm{510}.\: \\ $$$$ \\ $$$${if}\:{no}\:{book}\:{from}\:{S}\:{anf}\:{B}\:{is}\:{also} \\ $$$${allowed},\:{then}\:{the}\:{answer}\:{is}\:{the} \\ $$$${coefficient}\:{of}\:{x}^{\mathrm{17}} \:{term}\:{in} \\ $$$$\mathrm{17}!\left(\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}+\frac{{x}^{\mathrm{4}} }{\mathrm{4}!}+\frac{{x}^{\mathrm{6}} }{\mathrm{6}!}+…\right)\left(\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}+\frac{{x}^{\mathrm{4}} }{\mathrm{4}!}+\frac{{x}^{\mathrm{5}} }{\mathrm{5}!}+…\right)\left(\mathrm{1}+{x}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}+\frac{{x}^{\mathrm{4}} }{\mathrm{4}!}\right) \\ $$$${which}\:{is}\:\mathrm{18}\:\mathrm{072}\:\mathrm{242}. \\ $$

Commented by mr W last updated on 25/Oct/23