1-3-x-2-x-2-4x-dx-

Question Number 198948 by ArifinTanjung last updated on 26/Oct/23

$$\int_{\mathrm{1}} ^{\mathrm{3}} \frac{\mathrm{x}−\mathrm{2}}{\mathrm{x}^{\mathrm{2}} −\mathrm{4x}}\:\mathrm{dx}=\:…. \\ $$

Answered by ajfour last updated on 26/Oct/23

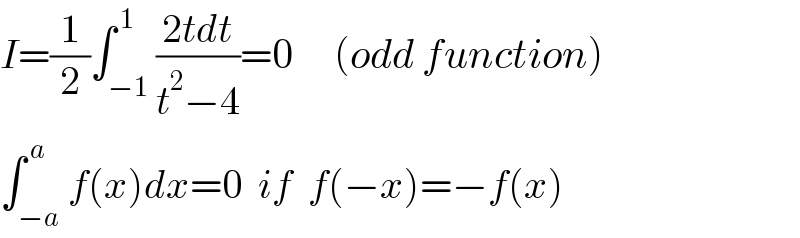
I=(1/2)∫_(−1) ^( 1) ((2tdt)/(t^2 −4))=0 (odd function) ∫_(−a) ^( a) f(x)dx=0 if f(−x)=−f(x)

$${I}=\frac{\mathrm{1}}{\mathrm{2}}\int_{−\mathrm{1}} ^{\:\mathrm{1}} \frac{\mathrm{2}{tdt}}{{t}^{\mathrm{2}} −\mathrm{4}}=\mathrm{0}\:\:\:\:\:\left({odd}\:{function}\right) \\ $$$$\int_{−{a}} ^{\:{a}} {f}\left({x}\right){dx}=\mathrm{0}\:\:{if}\:\:{f}\left(−{x}\right)=−{f}\left({x}\right) \\ $$

Answered by mr W last updated on 26/Oct/23

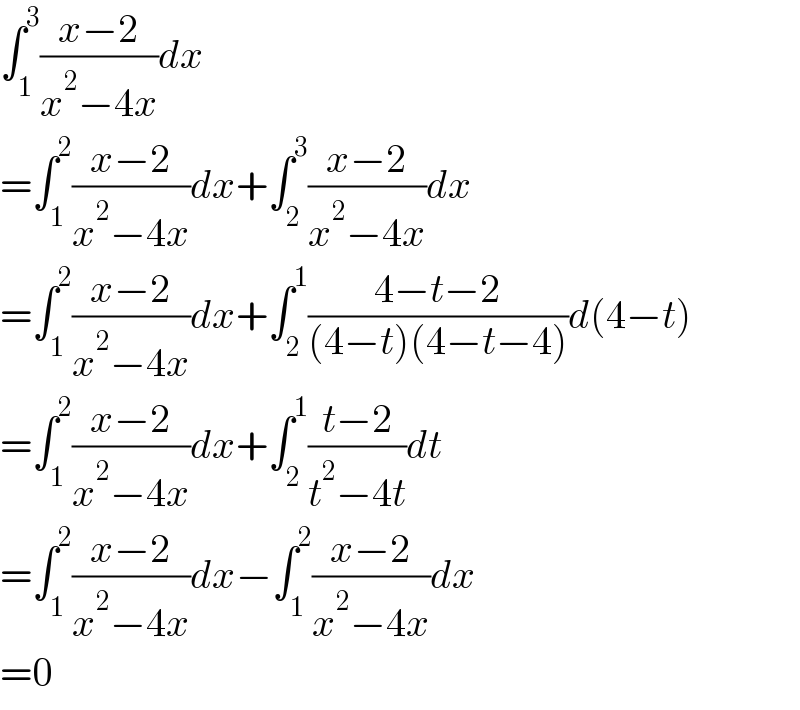
∫_1 ^3 ((x−2)/(x^2 −4x))dx =∫_1 ^2 ((x−2)/(x^2 −4x))dx+∫_2 ^3 ((x−2)/(x^2 −4x))dx =∫_1 ^2 ((x−2)/(x^2 −4x))dx+∫_2 ^1 ((4−t−2)/((4−t)(4−t−4)))d(4−t) =∫_1 ^2 ((x−2)/(x^2 −4x))dx+∫_2 ^1 ((t−2)/(t^2 −4t))dt =∫_1 ^2 ((x−2)/(x^2 −4x))dx−∫_1 ^2 ((x−2)/(x^2 −4x))dx =0

$$\int_{\mathrm{1}} ^{\mathrm{3}} \frac{{x}−\mathrm{2}}{{x}^{\mathrm{2}} −\mathrm{4}{x}}{dx} \\ $$$$=\int_{\mathrm{1}} ^{\mathrm{2}} \frac{{x}−\mathrm{2}}{{x}^{\mathrm{2}} −\mathrm{4}{x}}{dx}+\int_{\mathrm{2}} ^{\mathrm{3}} \frac{{x}−\mathrm{2}}{{x}^{\mathrm{2}} −\mathrm{4}{x}}{dx} \\ $$$$=\int_{\mathrm{1}} ^{\mathrm{2}} \frac{{x}−\mathrm{2}}{{x}^{\mathrm{2}} −\mathrm{4}{x}}{dx}+\int_{\mathrm{2}} ^{\mathrm{1}} \frac{\mathrm{4}−{t}−\mathrm{2}}{\left(\mathrm{4}−{t}\right)\left(\mathrm{4}−{t}−\mathrm{4}\right)}{d}\left(\mathrm{4}−{t}\right) \\ $$$$=\int_{\mathrm{1}} ^{\mathrm{2}} \frac{{x}−\mathrm{2}}{{x}^{\mathrm{2}} −\mathrm{4}{x}}{dx}+\int_{\mathrm{2}} ^{\mathrm{1}} \frac{{t}−\mathrm{2}}{{t}^{\mathrm{2}} −\mathrm{4}{t}}{dt} \\ $$$$=\int_{\mathrm{1}} ^{\mathrm{2}} \frac{{x}−\mathrm{2}}{{x}^{\mathrm{2}} −\mathrm{4}{x}}{dx}−\int_{\mathrm{1}} ^{\mathrm{2}} \frac{{x}−\mathrm{2}}{{x}^{\mathrm{2}} −\mathrm{4}{x}}{dx} \\ $$$$=\mathrm{0} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply