Question-199031

Question Number 199031 by cortano12 last updated on 27/Oct/23

Commented by AST last updated on 27/Oct/23

For 4, are the English or Mathematics books all different?

$${For}\:\mathrm{4},\:{are}\:{the}\:{English}\:{or}\:{Mathematics}\:{books} \\ $$$${all}\:{different}? \\ $$

Answered by mr W last updated on 27/Oct/23

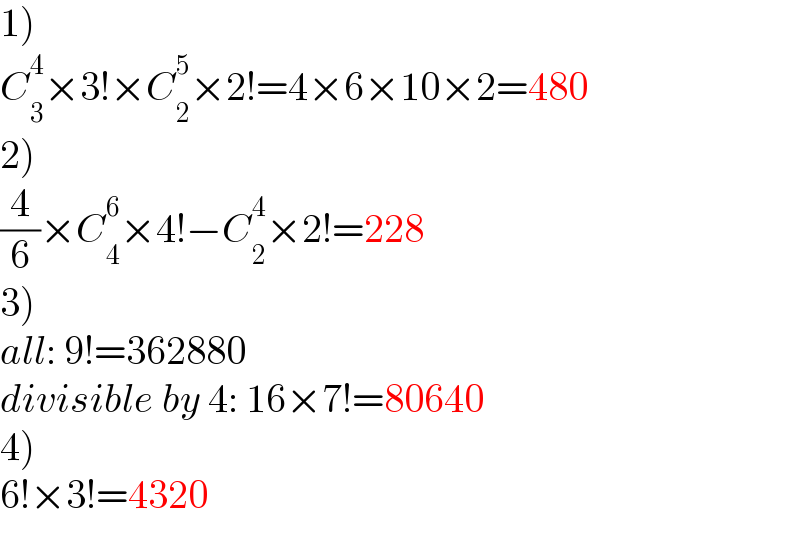
1) C_3 ^4 ×3!×C_2 ^5 ×2!=4×6×10×2=480 2) (4/6)×C_4 ^6 ×4!−C_2 ^4 ×2!=228 3) all: 9!=362880 divisible by 4: 16×7!=80640 4) 6!×3!=4320

$$\left.\mathrm{1}\right) \\ $$$${C}_{\mathrm{3}} ^{\mathrm{4}} ×\mathrm{3}!×{C}_{\mathrm{2}} ^{\mathrm{5}} ×\mathrm{2}!=\mathrm{4}×\mathrm{6}×\mathrm{10}×\mathrm{2}=\mathrm{480} \\ $$$$\left.\mathrm{2}\right) \\ $$$$\frac{\mathrm{4}}{\mathrm{6}}×{C}_{\mathrm{4}} ^{\mathrm{6}} ×\mathrm{4}!−{C}_{\mathrm{2}} ^{\mathrm{4}} ×\mathrm{2}!=\mathrm{228} \\ $$$$\left.\mathrm{3}\right) \\ $$$${all}:\:\mathrm{9}!=\mathrm{362880} \\ $$$${divisible}\:{by}\:\mathrm{4}:\:\mathrm{16}×\mathrm{7}!=\mathrm{80640} \\ $$$$\left.\mathrm{4}\right) \\ $$$$\mathrm{6}!×\mathrm{3}!=\mathrm{4320} \\ $$

Commented by cortano12 last updated on 27/Oct/23

$$\mathrm{explain}\:\mathrm{sir}\:\mathrm{why}\:\mathrm{16}×\mathrm{7}!\: \\ $$

Commented by mr W last updated on 27/Oct/23

abcdefgxy such that this number is divisible by 4, xy must be divisible by 4. there are 16 possiblities for xy: 12/16/24/28/32/36/48/52/56/64/68/72/76/84/92/96 to arrange the remaining 7 digits abcdefg there are 7! ways. so totally there are 16×7! valid numbers.

$${abcdefgxy} \\ $$$${such}\:{that}\:{this}\:{number}\:{is}\:{divisible} \\ $$$${by}\:\mathrm{4},\:{xy}\:{must}\:{be}\:{divisible}\:{by}\:\mathrm{4}.\:{there} \\ $$$${are}\:\mathrm{16}\:{possiblities}\:{for}\:{xy}: \\ $$$$\mathrm{12}/\mathrm{16}/\mathrm{24}/\mathrm{28}/\mathrm{32}/\mathrm{36}/\mathrm{48}/\mathrm{52}/\mathrm{56}/\mathrm{64}/\mathrm{68}/\mathrm{72}/\mathrm{76}/\mathrm{84}/\mathrm{92}/\mathrm{96} \\ $$$${to}\:{arrange}\:{the}\:{remaining}\:\mathrm{7}\:{digits} \\ $$$${abcdefg}\:{there}\:{are}\:\mathrm{7}!\:{ways}.\:{so}\:{totally} \\ $$$${there}\:{are}\:\mathrm{16}×\mathrm{7}!\:{valid}\:{numbers}. \\ $$

Commented by cortano12 last updated on 27/Oct/23

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}\: \\ $$

Answered by AST last updated on 27/Oct/23

1. (odd)(even)(odd)(even)(odd)=oeoeo ⇒4×4×3×3×2=288 oooeo⇒4×3×2×4×1=96 oeooo⇒4×4×3×2×1=96 ⇒#=480 2.abcd⇒a≥2,b≥1 or 0 b=1⇒4×4×3=48 b∈{2,3,4,5}⇒4×3×4×3=144⇒#=192 b=0⇒3×4×3=36⇒#=228 4. 6!×3!=4320

$$\mathrm{1}.\:\left({odd}\right)\left({even}\right)\left({odd}\right)\left({even}\right)\left({odd}\right)={oeoeo} \\ $$$$\Rightarrow\mathrm{4}×\mathrm{4}×\mathrm{3}×\mathrm{3}×\mathrm{2}=\mathrm{288} \\ $$$${oooeo}\Rightarrow\mathrm{4}×\mathrm{3}×\mathrm{2}×\mathrm{4}×\mathrm{1}=\mathrm{96} \\ $$$${oeooo}\Rightarrow\mathrm{4}×\mathrm{4}×\mathrm{3}×\mathrm{2}×\mathrm{1}=\mathrm{96} \\ $$$$\Rightarrow#=\mathrm{480} \\ $$$$\mathrm{2}.{abcd}\Rightarrow{a}\geqslant\mathrm{2},{b}\geqslant\mathrm{1}\:{or}\:\mathrm{0} \\ $$$${b}=\mathrm{1}\Rightarrow\mathrm{4}×\mathrm{4}×\mathrm{3}=\mathrm{48} \\ $$$${b}\in\left\{\mathrm{2},\mathrm{3},\mathrm{4},\mathrm{5}\right\}\Rightarrow\mathrm{4}×\mathrm{3}×\mathrm{4}×\mathrm{3}=\mathrm{144}\Rightarrow#=\mathrm{192} \\ $$$${b}=\mathrm{0}\Rightarrow\mathrm{3}×\mathrm{4}×\mathrm{3}=\mathrm{36}\Rightarrow#=\mathrm{228} \\ $$$$\mathrm{4}.\:\mathrm{6}!×\mathrm{3}!=\mathrm{4320} \\ $$

Commented by cortano12 last updated on 27/Oct/23

$$\mathrm{yes} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply