Question Number 199270 by mr W last updated on 31/Oct/23

Commented by mr W last updated on 31/Oct/23
$${an}\:{unsolved}\:{old}\:{question}\:#\mathrm{199155}. \\ $$
Commented by mr W last updated on 31/Oct/23

$${i}\:{got}\:\mathrm{1111}.\mathrm{1111}. \\ $$$${can}\:{someone}\:{comfirm}? \\ $$$${nikif}\mathrm{99}\:{sir}:\:{can}\:{you}\:{use}\:{your}\:{fortran} \\ $$$${program}\:{to}\:{check}\:{it}? \\ $$
Commented by nikif99 last updated on 31/Oct/23

$${I}\:{get}\:{mean}=\mathrm{1234}.\mathrm{43210678}. \\ $$$${ending}\:{digits}\:{in}\:{blue}\:{might}\:{be}\:“{noise}'' \\ $$$${of}\:{the}\:{processor}\:{or}\:{indeed}\:{decimal} \\ $$$${places}\:{when}\:{total}\:{divided}\:{by}\:\left(\mathrm{5}!×\mathrm{4}\right)=\mathrm{480}. \\ $$$${I}\:{will}\:{check}\:{it}\:{more}. \\ $$
Commented by mr W last updated on 31/Oct/23

$${thanks}\:{sirs}! \\ $$
Answered by aleks041103 last updated on 31/Oct/23
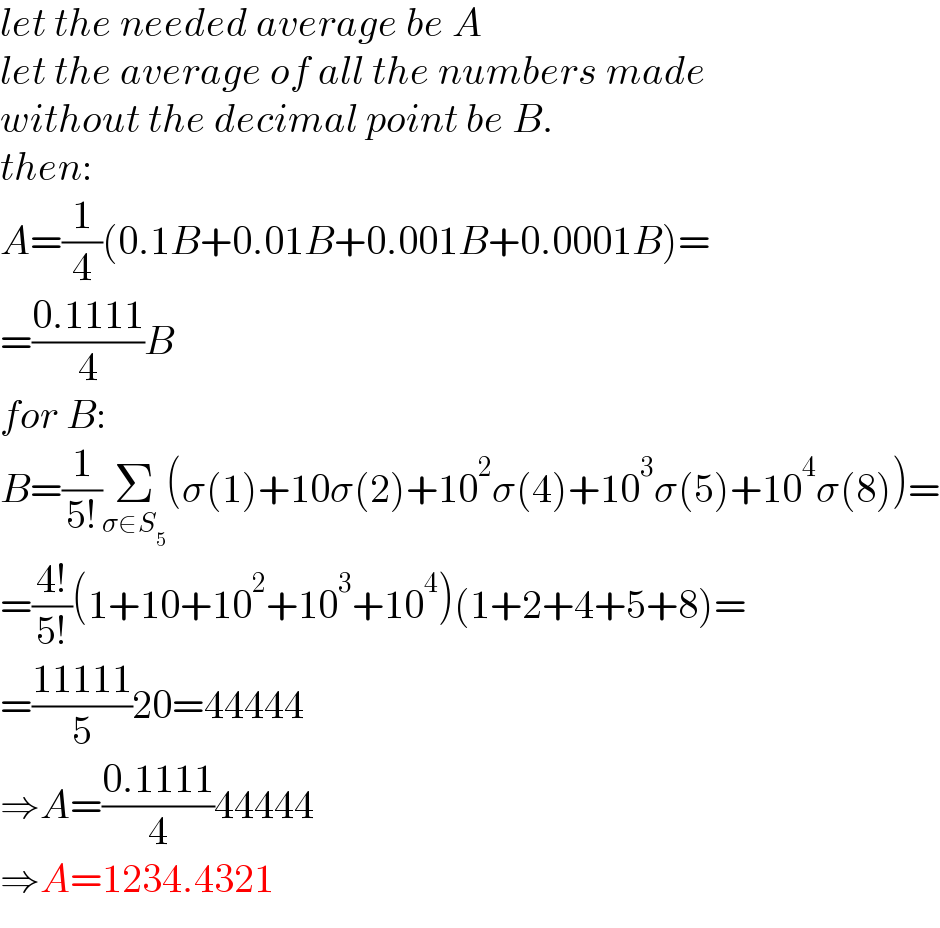
$${let}\:{the}\:{needed}\:{average}\:{be}\:{A} \\ $$$${let}\:{the}\:{average}\:{of}\:{all}\:{the}\:{numbers}\:{made} \\ $$$${without}\:{the}\:{decimal}\:{point}\:{be}\:{B}. \\ $$$${then}: \\ $$$${A}=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{0}.\mathrm{1}{B}+\mathrm{0}.\mathrm{01}{B}+\mathrm{0}.\mathrm{001}{B}+\mathrm{0}.\mathrm{0001}{B}\right)= \\ $$$$=\frac{\mathrm{0}.\mathrm{1111}}{\mathrm{4}}{B} \\ $$$${for}\:{B}: \\ $$$${B}=\frac{\mathrm{1}}{\mathrm{5}!}\underset{\sigma\in{S}_{\mathrm{5}} } {\sum}\left(\sigma\left(\mathrm{1}\right)+\mathrm{10}\sigma\left(\mathrm{2}\right)+\mathrm{10}^{\mathrm{2}} \sigma\left(\mathrm{4}\right)+\mathrm{10}^{\mathrm{3}} \sigma\left(\mathrm{5}\right)+\mathrm{10}^{\mathrm{4}} \sigma\left(\mathrm{8}\right)\right)= \\ $$$$=\frac{\mathrm{4}!}{\mathrm{5}!}\left(\mathrm{1}+\mathrm{10}+\mathrm{10}^{\mathrm{2}} +\mathrm{10}^{\mathrm{3}} +\mathrm{10}^{\mathrm{4}} \right)\left(\mathrm{1}+\mathrm{2}+\mathrm{4}+\mathrm{5}+\mathrm{8}\right)= \\ $$$$=\frac{\mathrm{11111}}{\mathrm{5}}\mathrm{20}=\mathrm{44444} \\ $$$$\Rightarrow{A}=\frac{\mathrm{0}.\mathrm{1111}}{\mathrm{4}}\mathrm{44444} \\ $$$$\Rightarrow{A}=\mathrm{1234}.\mathrm{4321} \\ $$
Commented by aleks041103 last updated on 31/Oct/23
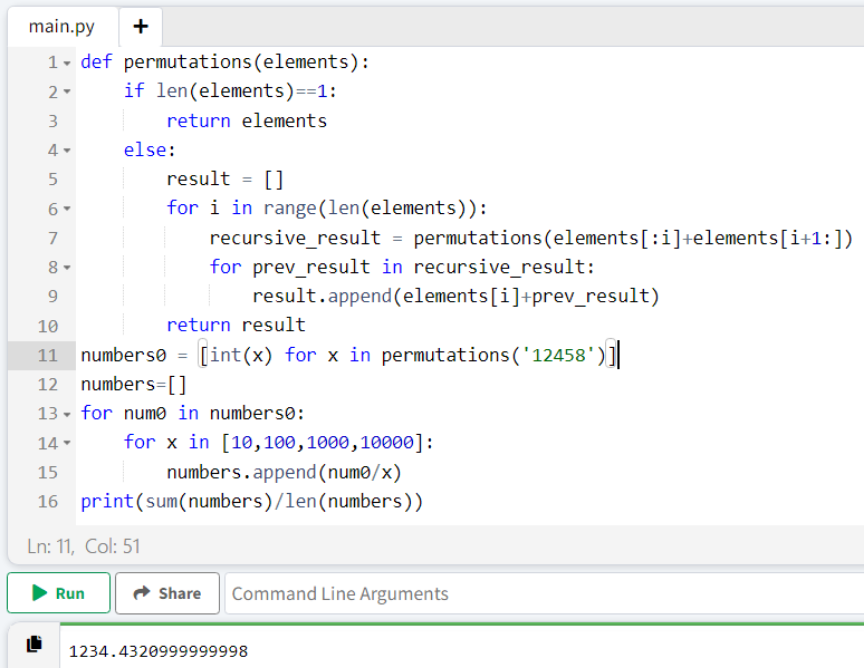
Commented by MathematicalUser2357 last updated on 04/Jan/24

$$\mathrm{CODING}\:\mathrm{TIME}! \\ $$
Answered by mr W last updated on 31/Oct/23

$${this}\:{is}\:{my}\:{solution}: \\ $$$${generallly},\:\:{the}\:{sum}\:{of}\:{some}\:{numbers} \\ $$$${is}\:{the}\:{sum}\:{of}\:{the}\:{values}\:{which}\:{their}\: \\ $$$${digits}\:{represent}.\:{for}\:{example}:\: \\ $$$$\mathrm{123}+\mathrm{132}+\mathrm{213}+\mathrm{231}+\mathrm{312}+\mathrm{321}=\mathrm{1332} \\ $$$${but}\:{we}\:{can}\:{also}\:{get}\:{the}\:{sum}\:{like}\:{this}: \\ $$$${the}\:{digit}\:“\mathrm{1}''\:{can}\:{stand}\:{on}\:{the}\:{first} \\ $$$${position}\:{which}\:{represents}\:\mathrm{100}.\:{there} \\ $$$${are}\:\mathrm{2}!\:{such}\:{possibilities}.\:{that}\:{means} \\ $$$${the}\:{sum}\:{of}\:{digit}\:“\mathrm{1}''\:{on}\:{the}\:{first}\: \\ $$$${position}\:{is}\:\mathrm{1}×\mathrm{100}×\mathrm{2}!.\:{the}\:{digit}\:“\mathrm{1}'' \\ $$$${can}\:{also}\:{stand}\:{on}\:{the}\:{second}\:{and} \\ $$$${the}\:{third}\:{position},\:{so}\:{the}\:{sum}\:{which} \\ $$$${the}\:{digit}\:“\mathrm{1}''\:{represents}\:{is} \\ $$$$\mathrm{1}×\left(\mathrm{100}+\mathrm{10}+\mathrm{1}\right)×\mathrm{2}!=\mathrm{1}×\mathrm{111}×\mathrm{2}! \\ $$$${and}\:{the}\:{sum}\:{which}\:{all}\:{didits}\:{present} \\ $$$${is}\:{thus} \\ $$$$\left(\mathrm{1}+\mathrm{2}+\mathrm{3}\right)×\mathrm{111}×\mathrm{2}!=\mathrm{6}×\mathrm{111}×\mathrm{2}=\mathrm{1332}. \\ $$$$ \\ $$$${now}\:{back}\:{to}\:{our}\:{question}. \\ $$$${with}\:{the}\:{digits}\:“\mathrm{1},\:\mathrm{2},\:\mathrm{4},\:\mathrm{5},\:\mathrm{8}''\:{and}\:{the}\: \\ $$$${decimal}\:{point}\:“.''\:{we}\:{can}\:{form}\:{totally} \\ $$$$\mathrm{5}!×\mathrm{4}=\mathrm{480}\:\:{numbers}.\:{each}\:{digit}\:“\mathrm{1}''\: \\ $$$${can}\:{represent}\:\mathrm{1000},\:\mathrm{100},\:\mathrm{10},\:\mathrm{1},\:\mathrm{0}.\mathrm{1},\: \\ $$$$\mathrm{0}.\mathrm{01},\:\mathrm{0}.\mathrm{001},\:\mathrm{0}.\mathrm{0001}\:{respectively}.\:{there}\: \\ $$$${are}\:\mathrm{4}!\:{possibilities}\:{for}\:{the}\:{digit}\:“\mathrm{1}''\:{on} \\ $$$$\mathrm{1000}{s}\:\:{position},\:\mathrm{2}×\mathrm{4}!\:{possibilities}\:{on} \\ $$$$\mathrm{100}{s}\:{position},\:\mathrm{3}×\mathrm{4}!\:{on}\:\mathrm{10}{s}\:{position}, \\ $$$$\mathrm{4}×\mathrm{4}!\:{on}\:\mathrm{1}{s}\:{position},\:\mathrm{4}×\mathrm{4}!\:{on}\:\mathrm{0}.\mathrm{1}{s} \\ $$$${position},\:\mathrm{3}×\mathrm{4}!\:{on}\:\mathrm{0}.\mathrm{01}{s}\:{position}, \\ $$$$\mathrm{2}×\mathrm{4}!\:{on}\:\mathrm{0}.\mathrm{001}{position}\:{and}\:\mathrm{1}×\mathrm{4}! \\ $$$${on}\:\mathrm{0}.\mathrm{0001}\:{position}.\:{so}\:{the}\:{sum} \\ $$$${which}\:{all}\:{digits}\:{represent}\:{is} \\ $$$$\left(\mathrm{1}+\mathrm{2}+\mathrm{4}+\mathrm{5}+\mathrm{8}\right)×\left(\mathrm{1}×\mathrm{1000}.\mathrm{0001}+\mathrm{2}×\mathrm{100}.\mathrm{001}+\mathrm{3}×\mathrm{10}.\mathrm{01}+\mathrm{4}×\mathrm{1}.\mathrm{1}\right)×\mathrm{4}! \\ $$$${so}\:{the}\:{average}\:{of}\:{the}\:{numbers}\:{is} \\ $$$$\frac{\left(\mathrm{1}+\mathrm{2}+\mathrm{4}+\mathrm{5}+\mathrm{8}\right)×\left(\mathrm{1}×\mathrm{1000}.\mathrm{0001}+\mathrm{2}×\mathrm{100}.\mathrm{001}+\mathrm{3}×\mathrm{10}.\mathrm{01}+\mathrm{4}×\mathrm{1}.\mathrm{1}\right)×\mathrm{4}!}{\mathrm{5}!×\mathrm{4}} \\ $$$$=\frac{\mathrm{20}×\left(\mathrm{1234}.\mathrm{4321}\right)}{\mathrm{5}×\mathrm{4}} \\ $$$$=\mathrm{1234}.\mathrm{4321}\:\checkmark \\ $$
Commented by aleks041103 last updated on 31/Oct/23

$${The}\:{poblem}\:{in}\:{your}\:{solution}\:{comes}\:{from}\:{the}\:{fact} \\ $$$${that}\:{yoy}\:{assume}\:{the}\:{digit}\:{can}\:{always}\:{represent} \\ $$$$\mathrm{0}.\mathrm{1},\:{which}\:{is}\:{incorrect}. \\ $$$${For}\:{example},\:{if}\:\mathrm{1}\:{is}\:{the}\:{first}\:{digit},\:{it}\:{cannot} \\ $$$${have}\:{a}\:{factor}\:\mathrm{0}.\mathrm{1},\:{because}\:{then}\:{the} \\ $$$${number}\:{would}\:{be}\:\mathrm{0}.\mathrm{1}…,\:{which}\:{is}\:{not} \\ $$$${allowed}\:{in}\:{the}\:{statement}. \\ $$
Commented by mr W last updated on 31/Oct/23
$${i}\:{didn}'{t}\:{assume}\:{that}.\:{it}\:{just}\:{meant} \\ $$$${that}\:“\mathrm{1}''\:{can}\:{stand}\:\:{for}\:\mathrm{0}.\mathrm{1},\:{for} \\ $$$${example}\:{in}\:{the}\:{numbers}\:{like} \\ $$$$\mathrm{2458}.\mathrm{1},\:\mathrm{4528}.\mathrm{1},\:{etc}. \\ $$
Commented by aleks041103 last updated on 31/Oct/23

$${yes}.\:{you}\:{are}\:{right}. \\ $$$${actually}\:{there}\:{is}\:{another}\:{problem}. \\ $$$${you}\:{assume}\:{there}\:{are}\:\mathrm{4}!\:{ways}\:{to}\:{have}\:'\mathrm{1}' \\ $$$${at}\:{the}\:\mathrm{10}{s}\:{position},\:{for}\:{example}. \\ $$$${this}\:{is}\:{true}\:{in}\:{the}\:{case}\:{of}\:{integers},\: \\ $$$${but}\:{the}\:{addition}\:{of}\:{the}\:{decimal}\:{dot}\: \\ $$$${changes}\:{things}. \\ $$$${example} \\ $$$$\mathrm{1}\:{in}\:\mathrm{10}{s}\:{position} \\ $$$$\left.\mathrm{1}\right)\:\ast\ast\ast\mathrm{1}\ast. \\ $$$$\left.\mathrm{2}\right)\:\ast\ast\mathrm{1}\ast.\ast \\ $$$$\left.\mathrm{3}\right)\:\ast\mathrm{1}\ast.\ast\ast \\ $$$$\left.\mathrm{4}\right)\:\mathrm{1}\ast.\ast\ast\ast \\ $$$${So}\:{actually}\:{for}\:{the}\:\mathrm{10}{s},\:{there}\:{are}\:{not}\:\mathrm{4}! \\ $$$${ways},\:{but}\:{actually}\:\mathrm{4}×\mathrm{4}!\:{ways}. \\ $$
Commented by mr W last updated on 31/Oct/23
$$\:{i}\:{got}\:{it}!\:{thank}\:{you}\:{sir}!\:{i}\:{have}\:{fixed} \\ $$$${my}\:{solution}\:{and}\:{got}\:{also}\:\mathrm{1234}.\mathrm{4321} \\ $$$${now}. \\ $$
