Question Number 199333 by necx122 last updated on 01/Nov/23
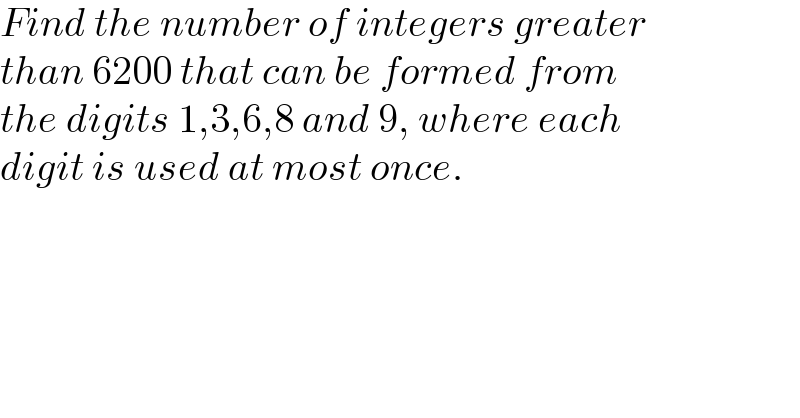
$${Find}\:{the}\:{number}\:{of}\:{integers}\:{greater} \\ $$$${than}\:\mathrm{6200}\:{that}\:{can}\:{be}\:{formed}\:{from} \\ $$$${the}\:{digits}\:\mathrm{1},\mathrm{3},\mathrm{6},\mathrm{8}\:{and}\:\mathrm{9},\:{where}\:{each} \\ $$$${digit}\:{is}\:{used}\:{at}\:{most}\:{once}. \\ $$
Answered by aleks041103 last updated on 01/Nov/23

$${Case}\:\mathrm{1}:\:\mathrm{4}−{digit}\:{nums} \\ $$$${The}\:{first}\:{digit}\:{can}\:{be}\:{only}\:\mathrm{6},\mathrm{8}\:{or}\:\mathrm{9}. \\ $$$${Case}\:\mathrm{1}.\mathrm{1}:\:\mathrm{8}\:{or}\:\mathrm{9} \\ $$$${we}\:{have}\:\mathrm{4}\:{digits}\:{left}\:{for}\:\mathrm{3}\:{positions}. \\ $$$$\Rightarrow{in}\:{total}=\mathrm{2}×\left(\mathrm{4}×\mathrm{3}×\mathrm{2}\right)=\mathrm{48} \\ $$$${Case}\:\mathrm{1}.\mathrm{2}:\:\mathrm{6} \\ $$$${the}\:{number}\:{can}\:{be}\:{of}\:{types}: \\ $$$$\mathrm{63}\ast\ast,\:\mathrm{68}\ast\ast,\mathrm{69}\ast\ast \\ $$$${for}\:{each}\:{of}\:{which}\:{we}\:{have}\:\mathrm{6}\:{options} \\ $$$$\Rightarrow{in}\:{total}=\mathrm{3}×\mathrm{6}=\mathrm{18} \\ $$$$ \\ $$$${Case}\mathrm{2}:\:\mathrm{5}−{digit}\:{nums} \\ $$$${All}\:\mathrm{5}−{digit}\:{are}\:{greater}\:{thn}\:\mathrm{6200}. \\ $$$$\Rightarrow{in}\:{total}=\mathrm{5}×\mathrm{4}×\mathrm{3}×\mathrm{2}×\mathrm{1}=\mathrm{120} \\ $$$$ \\ $$$${Answer}=\mathrm{48}+\mathrm{18}+\mathrm{120} \\ $$$$ \\ $$$$\Rightarrow{Ans}.=\mathrm{186} \\ $$
Commented by necx122 last updated on 01/Nov/23
Thank you. This reminds me of how I learnt this those days with Mr. W's method. Thank you so much our old friend, Aleks.
Answered by mr W last updated on 01/Nov/23

$$\left.\mathrm{1}\right)\:\mathrm{5}−{digit}\:{numbers}: \\ $$$$\mathrm{5}!=\mathrm{120} \\ $$$$ \\ $$$$\left.\mathrm{2}\right)\:{valid}\:\mathrm{4}−{digit}\:{numbers}: \\ $$$$\mathrm{63}{xy},\:\mathrm{68}{xy},\:\mathrm{69}{xy}, \\ $$$$\mathrm{81}{xy},\:\mathrm{83}{xy},\:\mathrm{86}{xy},\:\mathrm{89}{xy}, \\ $$$$\mathrm{91}{xy},\:\mathrm{93}{xy},\:\mathrm{96}{xy},\:\mathrm{98}{xy} \\ $$$${xy}=\mathrm{2}\:{from}\:\mathrm{3}={P}_{\mathrm{2}} ^{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{11}×{P}_{\mathrm{2}} ^{\mathrm{3}} =\mathrm{66} \\ $$$$ \\ $$$${totally}:\:\mathrm{120}+\mathrm{66}=\mathrm{186}\:\checkmark \\ $$
Commented by necx122 last updated on 01/Nov/23
always on it sir. Thank you. This is clear and well understood.
