Question Number 199353 by mr W last updated on 01/Nov/23

$${What}\:{is}\:{the}\:{probability}\:{that}\:{in}\:{a}\:{class}\: \\ $$$${of}\:\mathrm{18}\:{people},\:{there}\:{exists}\:{exactly}\:{a}\: \\ $$$${group}\:{of}\:{exactly}\:\mathrm{3}\:{people}\:{born}\:{on}\:{the} \\ $$$${same}\:{day}\:{of}\:{the}\:{week}? \\ $$
Commented by AST last updated on 01/Nov/23

$$\frac{{C}_{\mathrm{3}} ^{\mathrm{18}} ×\mathrm{6}^{\mathrm{15}} }{\mathrm{7}^{\mathrm{18}} }\approx\mathrm{0}.\mathrm{23561} \\ $$
Commented by nikif99 last updated on 03/Nov/23
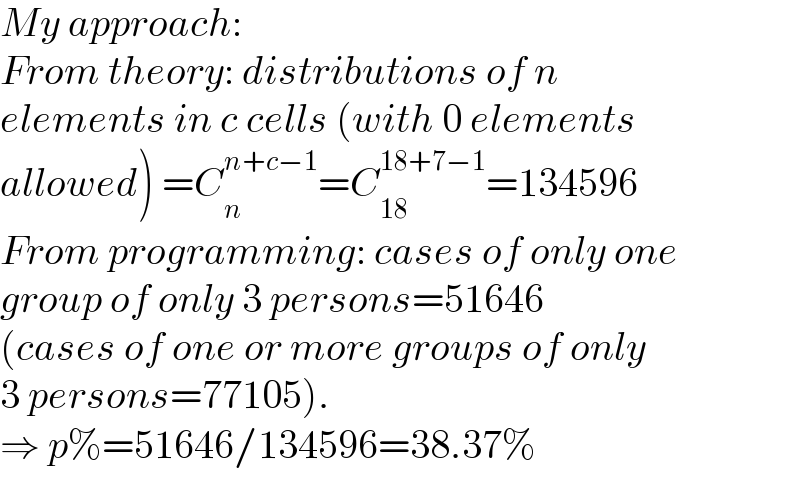
$${My}\:{approach}: \\ $$$${From}\:{theory}:\:{distributions}\:{of}\:{n} \\ $$$${elements}\:{in}\:{c}\:{cells}\:\left({with}\:\mathrm{0}\:{elements}\right. \\ $$$$\left.{allowed}\right)\:={C}_{{n}} ^{{n}+{c}−\mathrm{1}} ={C}_{\mathrm{18}} ^{\mathrm{18}+\mathrm{7}−\mathrm{1}} =\mathrm{134596} \\ $$$${From}\:{programming}:\:{cases}\:{of}\:{only}\:{one} \\ $$$${group}\:{of}\:{only}\:\mathrm{3}\:{persons}=\mathrm{51646} \\ $$$$\left({cases}\:{of}\:{one}\:{or}\:{more}\:{groups}\:{of}\:{only}\right. \\ $$$$\left.\mathrm{3}\:{persons}=\mathrm{77105}\right). \\ $$$$\Rightarrow\:{p\%}=\mathrm{51646}/\mathrm{134596}=\mathrm{38}.\mathrm{37\%} \\ $$
Commented by AST last updated on 03/Nov/23
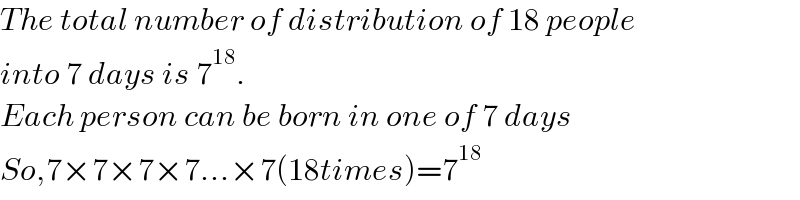
$${The}\:{total}\:{number}\:{of}\:{distribution}\:{of}\:\mathrm{18}\:{people} \\ $$$${into}\:\mathrm{7}\:{days}\:{is}\:\mathrm{7}^{\mathrm{18}} . \\ $$$${Each}\:{person}\:{can}\:{be}\:{born}\:{in}\:{one}\:{of}\:\mathrm{7}\:{days} \\ $$$${So},\mathrm{7}×\mathrm{7}×\mathrm{7}×\mathrm{7}…×\mathrm{7}\left(\mathrm{18}{times}\right)=\mathrm{7}^{\mathrm{18}} \\ $$
Commented by AST last updated on 03/Nov/23
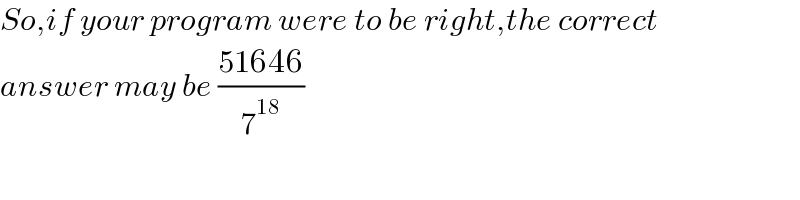
$${So},{if}\:{your}\:{program}\:{were}\:{to}\:{be}\:{right},{the}\:{correct} \\ $$$${answer}\:{may}\:{be}\:\frac{\mathrm{51646}}{\mathrm{7}^{\mathrm{18}} } \\ $$
Commented by nikif99 last updated on 03/Nov/23

$${You}\:{are}\:{right}.\:{The}\:{formula}\:{I}\:{used} \\ $$$${refers}\:{to}\:{non}\:{distinctif}\:{elements}. \\ $$$${For}\:{distinctif}\:{elements}\:{is}\:{c}^{{n}} . \\ $$
