Question Number 199781 by cortano12 last updated on 09/Nov/23

$$\:\:\: \\ $$
Answered by qaz last updated on 09/Nov/23
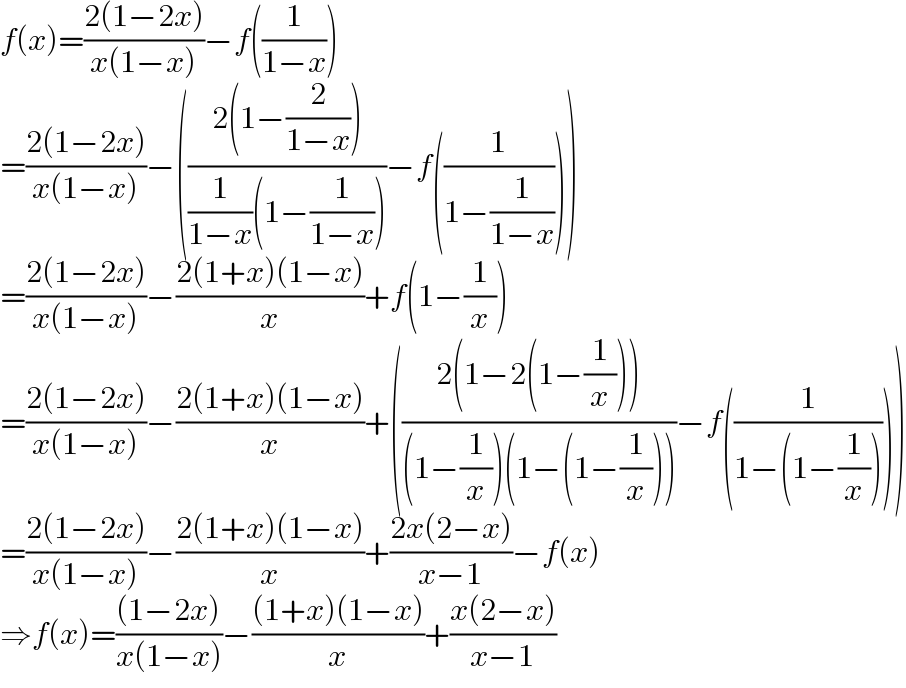
$${f}\left({x}\right)=\frac{\mathrm{2}\left(\mathrm{1}−\mathrm{2}{x}\right)}{{x}\left(\mathrm{1}−{x}\right)}−{f}\left(\frac{\mathrm{1}}{\mathrm{1}−{x}}\right) \\ $$$$=\frac{\mathrm{2}\left(\mathrm{1}−\mathrm{2}{x}\right)}{{x}\left(\mathrm{1}−{x}\right)}−\left(\frac{\mathrm{2}\left(\mathrm{1}−\frac{\mathrm{2}}{\mathrm{1}−{x}}\right)}{\frac{\mathrm{1}}{\mathrm{1}−{x}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}−{x}}\right)}−{f}\left(\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}−{x}}}\right)\right) \\ $$$$=\frac{\mathrm{2}\left(\mathrm{1}−\mathrm{2}{x}\right)}{{x}\left(\mathrm{1}−{x}\right)}−\frac{\mathrm{2}\left(\mathrm{1}+{x}\right)\left(\mathrm{1}−{x}\right)}{{x}}+{f}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right) \\ $$$$=\frac{\mathrm{2}\left(\mathrm{1}−\mathrm{2}{x}\right)}{{x}\left(\mathrm{1}−{x}\right)}−\frac{\mathrm{2}\left(\mathrm{1}+{x}\right)\left(\mathrm{1}−{x}\right)}{{x}}+\left(\frac{\mathrm{2}\left(\mathrm{1}−\mathrm{2}\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right)\right)}{\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right)\left(\mathrm{1}−\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right)\right)}−{f}\left(\frac{\mathrm{1}}{\mathrm{1}−\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right)}\right)\right) \\ $$$$=\frac{\mathrm{2}\left(\mathrm{1}−\mathrm{2}{x}\right)}{{x}\left(\mathrm{1}−{x}\right)}−\frac{\mathrm{2}\left(\mathrm{1}+{x}\right)\left(\mathrm{1}−{x}\right)}{{x}}+\frac{\mathrm{2}{x}\left(\mathrm{2}−{x}\right)}{{x}−\mathrm{1}}−{f}\left({x}\right) \\ $$$$\Rightarrow{f}\left({x}\right)=\frac{\left(\mathrm{1}−\mathrm{2}{x}\right)}{{x}\left(\mathrm{1}−{x}\right)}−\frac{\left(\mathrm{1}+{x}\right)\left(\mathrm{1}−{x}\right)}{{x}}+\frac{{x}\left(\mathrm{2}−{x}\right)}{{x}−\mathrm{1}} \\ $$
Commented by Frix last updated on 09/Nov/23
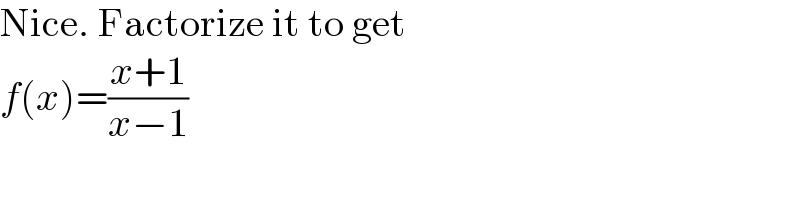
$$\mathrm{Nice}.\:\mathrm{Factorize}\:\mathrm{it}\:\mathrm{to}\:\mathrm{get} \\ $$$${f}\left({x}\right)=\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}} \\ $$
Commented by cortano12 last updated on 10/Nov/23

$$\mathrm{yes}….\mathrm{nice} \\ $$
Commented by York12 last updated on 10/Nov/23

$$ \\ $$$$\mathrm{Bruh}\:\mathrm{where}\:\mathrm{to}\:\mathrm{learn}\:\mathrm{functional}\:\mathrm{equations} \\ $$
