Question Number 200048 by Calculusboy last updated on 12/Nov/23
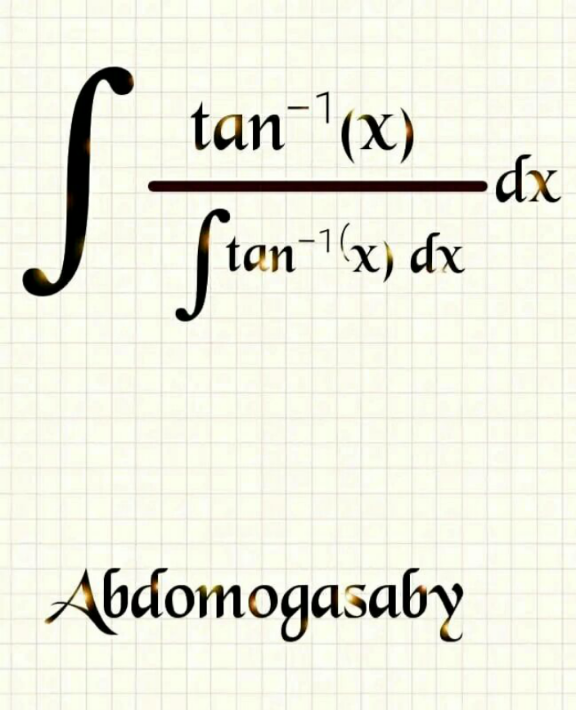
Commented by 0670322918 last updated on 13/Nov/23

$$\int\frac{{tan}^{−\mathrm{1}} \left({x}\right)}{\int{tan}^{−\mathrm{1}} \left({x}\right){dx}}{dx}= \\ $$$${f}\left({x}\right)=\int{tan}^{−\mathrm{1}} \left({x}\right){dx}={xtan}^{−\mathrm{1}} \left({x}\right)−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({x}^{\mathrm{2}} +\mathrm{1}\right)+{c} \\ $$$${f}'\left({x}\right)={tan}^{−\mathrm{1}} \left({x}\right) \\ $$$$\int\frac{{f}'\left({x}\right)}{{f}\left({x}\right)}{dx}={ln}\mid{f}\left({x}\right)\mid+{c} \\ $$$$\int\frac{{tan}^{−\mathrm{1}} \left({x}\right)}{\int{tan}^{−\mathrm{1}} \left({x}\right){dx}}{dx}={ln}\mid{xtan}^{−\mathrm{1}} \left({x}\right)−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({x}^{\mathrm{2}} +\mathrm{1}\right)+{c}\mid+{c}_{\mathrm{1}} \\ $$$$ \\ $$
Commented by Calculusboy last updated on 13/Nov/23

$$\boldsymbol{{thanks}}\:\boldsymbol{{sir}} \\ $$
