Question Number 200051 by cortano12 last updated on 13/Nov/23

$$ \\ $$$$\mathrm{There}\:\mathrm{are}\:\mathrm{many}\:\mathrm{ways}\:\mathrm{to}\:\mathrm{arrange}\:\mathrm{3}\:\mathrm{red} \\ $$$$\:\mathrm{balls}\:\mathrm{and}\:\mathrm{9}\:\mathrm{black}\:\mathrm{balls}\:\mathrm{in}\:\mathrm{a}\:\mathrm{circle}\: \\ $$$$\mathrm{so}\:\mathrm{that}\:\mathrm{there}\:\mathrm{are}\:\mathrm{a}\:\mathrm{minimum}\:\mathrm{of}\:\mathrm{2} \\ $$$$\mathrm{black}\:\mathrm{balls}\:\mathrm{between}\:\mathrm{2}\:\mathrm{adjacent}\:\mathrm{red} \\ $$$$\mathrm{balls}. \\ $$$$\left(\mathrm{a}\right)\:\mathrm{180}×\mathrm{8}!\:\:\:\:\left(\mathrm{b}\right)\:\mathrm{240}×\mathrm{7}!\:\:\:\:\left(\mathrm{c}\right)\:\mathrm{364}×\mathrm{6}! \\ $$$$\:\left(\mathrm{d}\right)\:\mathrm{282}×\mathrm{4}!\:\:\:\:\left(\mathrm{e}\right)\:\mathrm{144}×\mathrm{5}!\: \\ $$
Commented by mr W last updated on 13/Nov/23

$${different}\:{or}\:{identical}\:{balls}? \\ $$
Commented by cortano12 last updated on 13/Nov/23

$$\mathrm{different}\:\mathrm{balls} \\ $$
Answered by mr W last updated on 13/Nov/23

$${to}\:{arrange}\:{the}\:{red}\:{balls}:\:\mathrm{2}!=\mathrm{2} \\ $$$${to}\:{arrange}\:{the}\:{black}\:{balls}: \\ $$$$\mathrm{2}+\mathrm{2}+\mathrm{5}\:\Rightarrow\frac{\mathrm{3}!}{\mathrm{2}!}×\mathrm{2}!×\mathrm{2}!×\mathrm{5}!=\mathrm{1440} \\ $$$$\mathrm{2}+\mathrm{3}+\mathrm{4}\:\Rightarrow\mathrm{3}!×\mathrm{2}!×\mathrm{3}!×\mathrm{4}!=\mathrm{1728} \\ $$$$\mathrm{3}+\mathrm{3}+\mathrm{3}\:\Rightarrow\mathrm{3}!×\mathrm{3}!×\mathrm{3}!=\mathrm{216} \\ $$$$\Rightarrow\mathrm{2}×\left(\mathrm{1440}+\mathrm{1728}+\mathrm{216}\right)=\mathrm{6768}\:\checkmark \\ $$$$\Rightarrow{answer}\:\left({d}\right) \\ $$
Commented by cortano12 last updated on 13/Nov/23
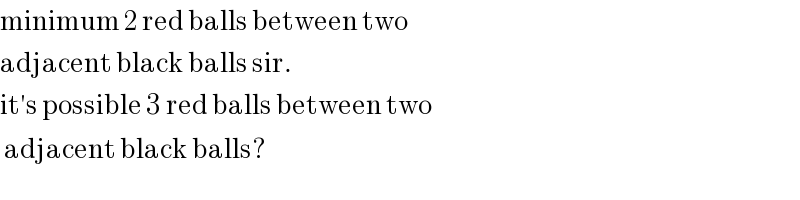
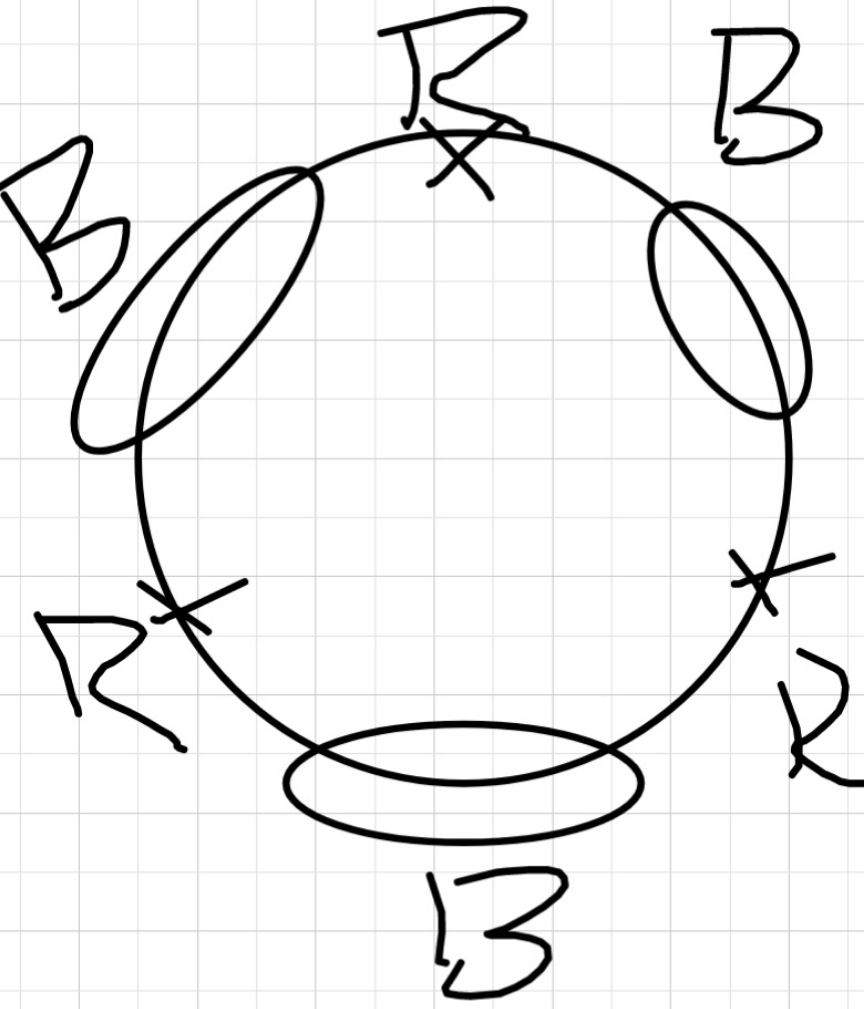
$$\mathrm{minimum}\:\mathrm{2}\:\mathrm{red}\:\mathrm{balls}\:\mathrm{between}\:\mathrm{two}\: \\ $$$$\mathrm{adjacent}\:\mathrm{black}\:\mathrm{balls}\:\mathrm{sir}. \\ $$$$\mathrm{it}'\mathrm{s}\:\mathrm{possible}\:\mathrm{3}\:\mathrm{red}\:\mathrm{balls}\:\mathrm{between}\:\mathrm{two} \\ $$$$\:\mathrm{adjacent}\:\mathrm{black}\:\mathrm{balls}? \\ $$
Commented by mr W last updated on 13/Nov/23

$${no},\:\:\mathrm{2},\:\mathrm{3},\:\mathrm{4}\:{or}\:\mathrm{5}\:\boldsymbol{{black}}\:{balls}\:{between} \\ $$$${two}\:\boldsymbol{{red}}\:{balls}\:{as}\:{the}\:{question}\:{requests}. \\ $$
Commented by cortano12 last updated on 13/Nov/23

$$\mathrm{l}\:\mathrm{got}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{A} \\ $$
Commented by cortano12 last updated on 13/Nov/23
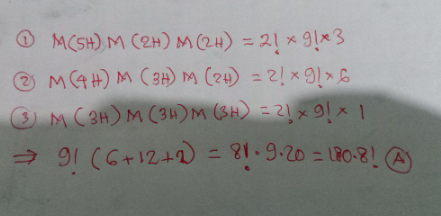
Commented by mr W last updated on 13/Nov/23
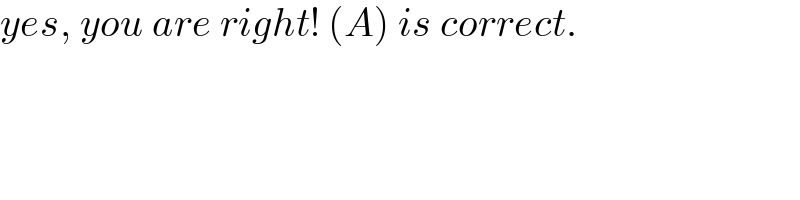
$${yes},\:{you}\:{are}\:{right}!\:\left({A}\right)\:{is}\:{correct}. \\ $$
Answered by MM42 last updated on 13/Nov/23
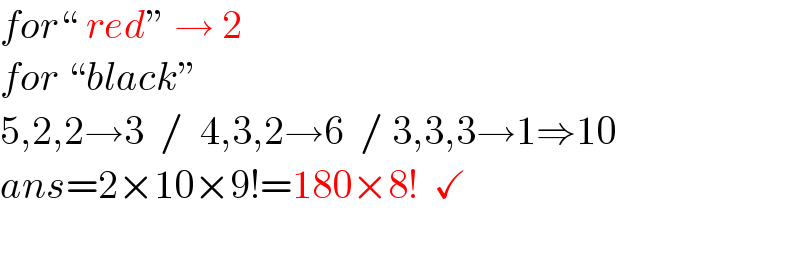
$${for}“\:{red}''\:\rightarrow\:\mathrm{2} \\ $$$${for}\:“{black}'' \\ $$$$\mathrm{5},\mathrm{2},\mathrm{2}\rightarrow\mathrm{3}\:\:/\:\:\mathrm{4},\mathrm{3},\mathrm{2}\rightarrow\mathrm{6}\:\:/\:\mathrm{3},\mathrm{3},\mathrm{3}\rightarrow\mathrm{1}\Rightarrow\mathrm{10} \\ $$$${ans}=\mathrm{2}×\mathrm{10}×\mathrm{9}!=\mathrm{180}×\mathrm{8}!\:\:\checkmark \\ $$$$ \\ $$
Commented by MM42 last updated on 13/Nov/23