Question Number 200103 by cortano12 last updated on 14/Nov/23
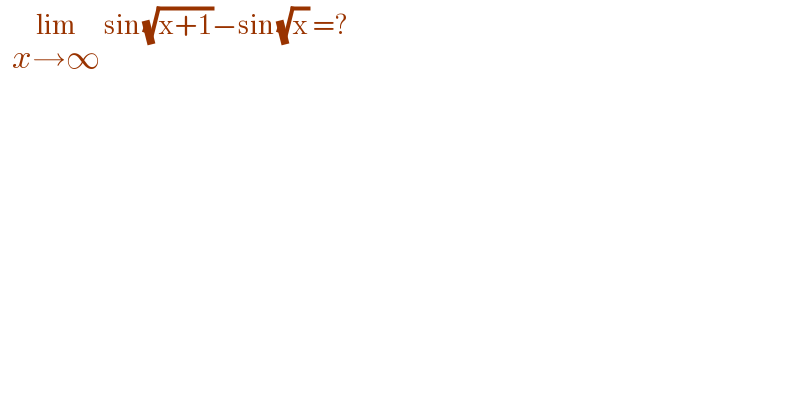
$$\:\:\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\mathrm{sin}\:\sqrt{\mathrm{x}+\mathrm{1}}−\mathrm{sin}\:\sqrt{\mathrm{x}}\:=? \\ $$
Answered by Frix last updated on 14/Nov/23
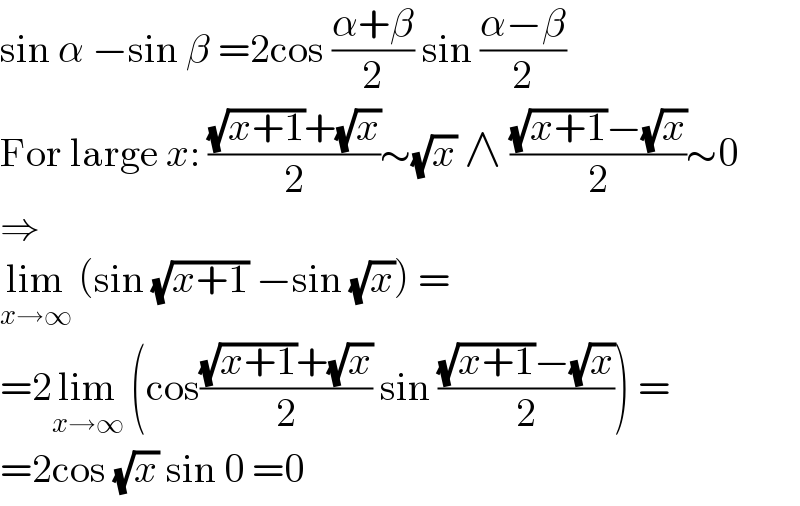
$$\mathrm{sin}\:\alpha\:−\mathrm{sin}\:\beta\:=\mathrm{2cos}\:\frac{\alpha+\beta}{\mathrm{2}}\:\mathrm{sin}\:\frac{\alpha−\beta}{\mathrm{2}} \\ $$$$\mathrm{For}\:\mathrm{large}\:{x}:\:\frac{\sqrt{{x}+\mathrm{1}}+\sqrt{{x}}}{\mathrm{2}}\sim\sqrt{{x}}\:\wedge\:\frac{\sqrt{{x}+\mathrm{1}}−\sqrt{{x}}}{\mathrm{2}}\sim\mathrm{0} \\ $$$$\Rightarrow \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(\mathrm{sin}\:\sqrt{{x}+\mathrm{1}}\:−\mathrm{sin}\:\sqrt{{x}}\right)\:= \\ $$$$=\mathrm{2}\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(\mathrm{cos}\frac{\sqrt{{x}+\mathrm{1}}+\sqrt{{x}}}{\mathrm{2}}\:\mathrm{sin}\:\frac{\sqrt{{x}+\mathrm{1}}−\sqrt{{x}}}{\mathrm{2}}\right)\:= \\ $$$$=\mathrm{2cos}\:\sqrt{{x}}\:\mathrm{sin}\:\mathrm{0}\:=\mathrm{0} \\ $$
