Question Number 200105 by cortano12 last updated on 14/Nov/23
Commented by mr W last updated on 14/Nov/23
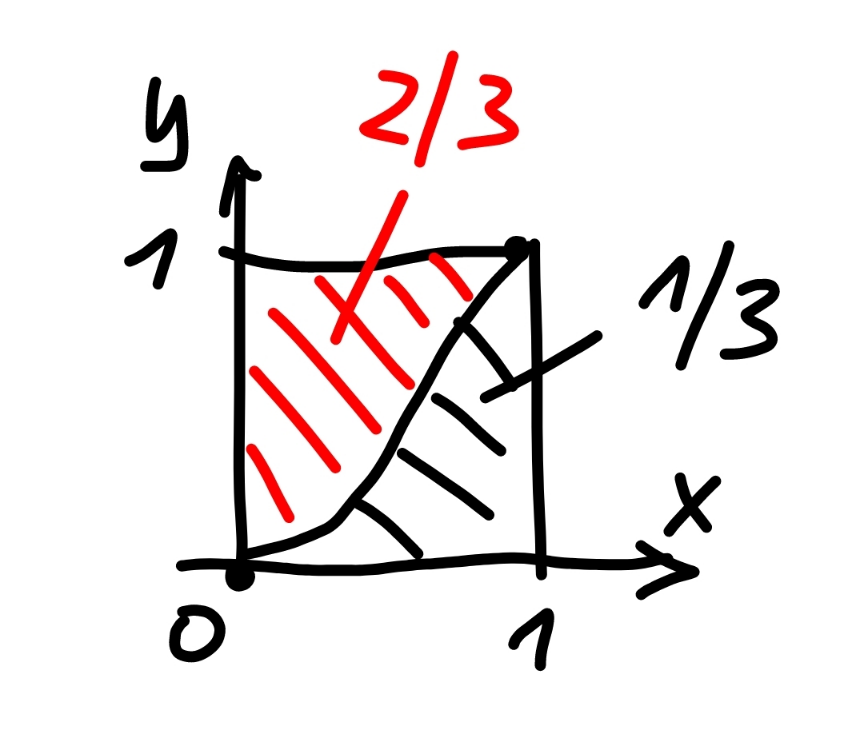
Commented by mr W last updated on 14/Nov/23
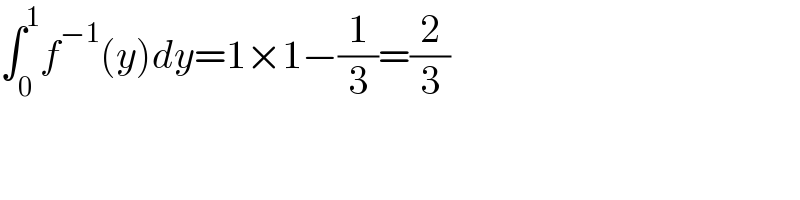
$$\int_{\mathrm{0}} ^{\mathrm{1}} {f}^{−\mathrm{1}} \left({y}\right){dy}=\mathrm{1}×\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}=\frac{\mathrm{2}}{\mathrm{3}} \\ $$
Answered by witcher3 last updated on 15/Nov/23
![∫_0 ^1 f^− (y)dy y=f(x) ∫_0 ^1 xf′(x)dx=[_0 ^1 xf(x)]−∫_0 ^1 f(x)=1−(1/3)=(2/3)](https://www.tinkutara.com/question/Q200123.png)
$$\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{f}^{−} \left(\mathrm{y}\right)\mathrm{dy} \\ $$$$\mathrm{y}=\mathrm{f}\left(\mathrm{x}\right) \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{xf}'\left(\mathrm{x}\right)\mathrm{dx}=\left[_{\mathrm{0}} ^{\mathrm{1}} \mathrm{xf}\left(\mathrm{x}\right)\right]−\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{f}\left(\mathrm{x}\right)=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}=\frac{\mathrm{2}}{\mathrm{3}} \\ $$
