Question Number 200412 by hardmath last updated on 18/Nov/23
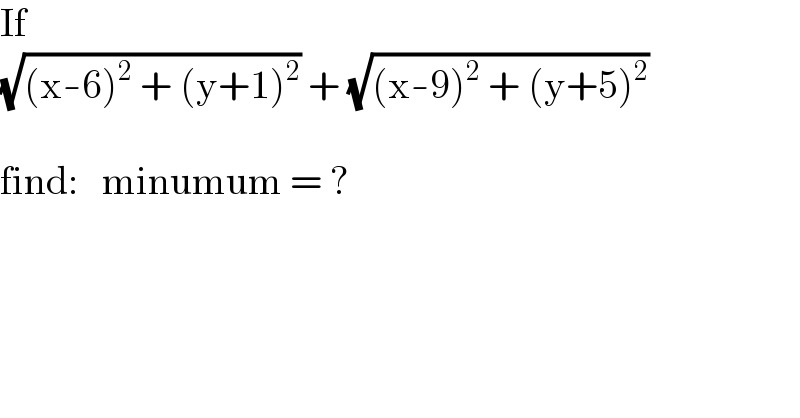
$$\mathrm{If} \\ $$$$\sqrt{\left(\mathrm{x}-\mathrm{6}\right)^{\mathrm{2}} \:+\:\left(\mathrm{y}+\mathrm{1}\right)^{\mathrm{2}} }\:+\:\sqrt{\left(\mathrm{x}-\mathrm{9}\right)^{\mathrm{2}} \:+\:\left(\mathrm{y}+\mathrm{5}\right)^{\mathrm{2}} } \\ $$$$ \\ $$$$\mathrm{find}:\:\:\:\mathrm{minumum}\:=\:? \\ $$
Answered by witcher3 last updated on 18/Nov/23
![A(6,−1);B=(9,−5) M(x,y) we want min AM+MB≥AB;∀M∈IR^2 AM+MB=AB ,∀M∈[AB] min=(√((6−9)^2 +(−1+5)^2 ))=(√(9+16 ))=5](https://www.tinkutara.com/question/Q200422.png)
$$\mathrm{A}\left(\mathrm{6},−\mathrm{1}\right);\mathrm{B}=\left(\mathrm{9},−\mathrm{5}\right) \\ $$$$\mathrm{M}\left(\mathrm{x},\mathrm{y}\right) \\ $$$$\mathrm{we}\:\mathrm{want}\:\mathrm{min}\:\mathrm{AM}+\mathrm{MB}\geqslant\mathrm{AB};\forall\mathrm{M}\in\mathrm{IR}^{\mathrm{2}} \\ $$$$\mathrm{AM}+\mathrm{MB}=\mathrm{AB}\:,\forall\mathrm{M}\in\left[\mathrm{AB}\right] \\ $$$$\mathrm{min}=\sqrt{\left(\mathrm{6}−\mathrm{9}\right)^{\mathrm{2}} +\left(−\mathrm{1}+\mathrm{5}\right)^{\mathrm{2}} }=\sqrt{\mathrm{9}+\mathrm{16}\:}=\mathrm{5} \\ $$
Commented by hardmath last updated on 18/Nov/23

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{dear}\:\mathrm{professor} \\ $$
