Menu Close

Question-200413

Tinku Tara 0 Comments
Pin




Question Number 200413 by Mingma last updated on 18/Nov/23
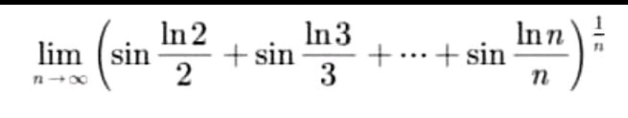
Commented by Mingma last updated on 18/Nov/23
Evaluate!
Answered by witcher3 last updated on 18/Nov/23
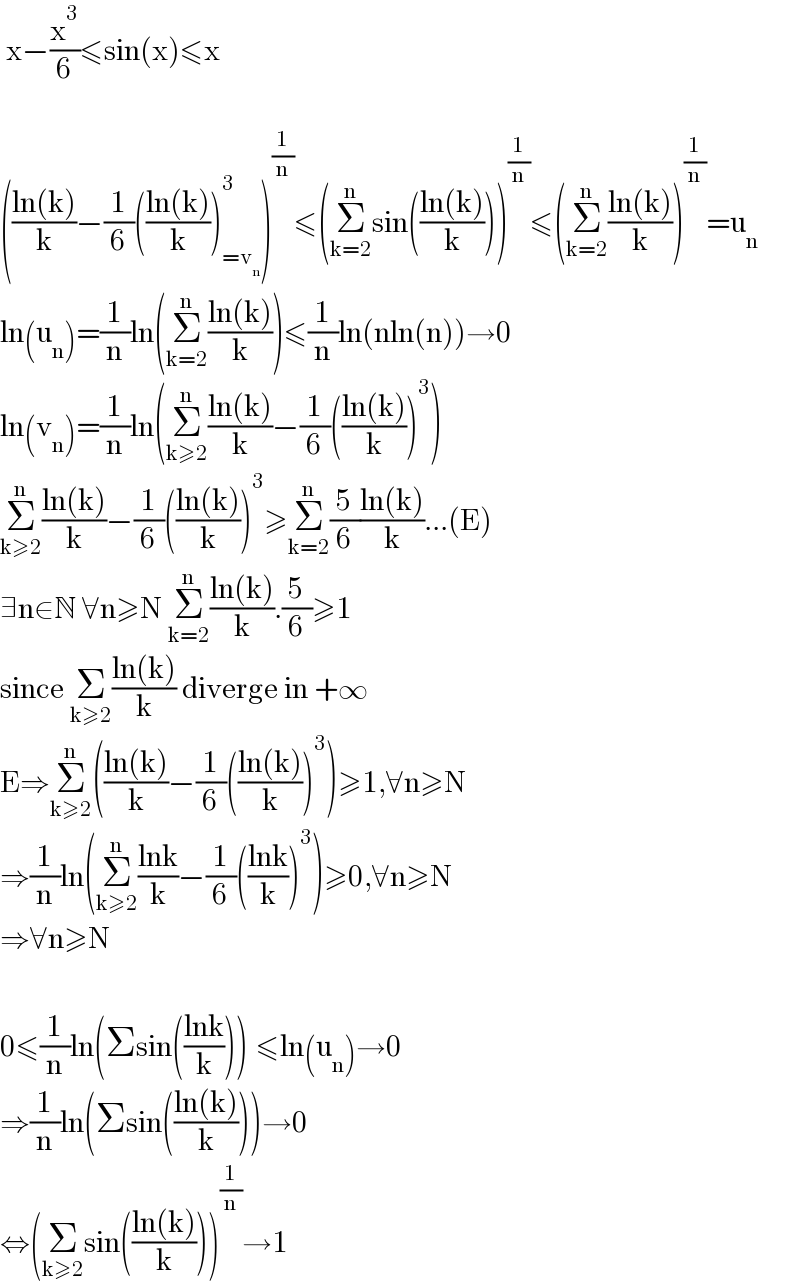
x−(x^3 /6)≤sin(x)≤x (((ln(k))/k)−(1/6)(((ln(k))/k))_(=v_n ) ^3 )^(1/n) ≤(Σ_(k=2) ^n sin(((ln(k))/k)))^(1/n) ≤(Σ_(k=2) ^n ((ln(k))/k))^(1/n) =u_n ln(u_n )=(1/n)ln(Σ_(k=2) ^n ((ln(k))/k))≤(1/n)ln(nln(n))→0 ln(v_n )=(1/n)ln(Σ_(k≥2) ^n ((ln(k))/k)−(1/6)(((ln(k))/k))^3 ) Σ_(k≥2) ^n ((ln(k))/k)−(1/6)(((ln(k))/k))^3 ≥Σ_(k=2) ^n (5/6)((ln(k))/k)...(E) ∃n∈N ∀n≥N Σ_(k=2) ^n ((ln(k))/k).(5/6)≥1 since Σ_(k≥2) ((ln(k))/k) diverge in +∞ E⇒Σ_(k≥2) ^n (((ln(k))/k)−(1/6)(((ln(k))/k))^3 )≥1,∀n≥N ⇒(1/n)ln(Σ_(k≥2) ^n ((lnk)/k)−(1/6)(((lnk)/k))^3 )≥0,∀n≥N ⇒∀n≥N 0≤(1/n)ln(Σsin(((lnk)/k)))^ ≤ln(u_n )→0 ⇒(1/n)ln(Σsin(((ln(k))/k)))→0 ⇔(Σ_(k≥2) sin(((ln(k))/k)))^(1/n) →1
$$\:\mathrm{x}−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{6}}\leqslant\mathrm{sin}\left(\mathrm{x}\right)\leqslant\mathrm{x} \\ $$$$ \\ $$$$\left(\frac{\mathrm{ln}\left(\mathrm{k}\right)}{\mathrm{k}}−\frac{\mathrm{1}}{\mathrm{6}}\left(\frac{\mathrm{ln}\left(\mathrm{k}\right)}{\mathrm{k}}\right)_{=\mathrm{v}_{\mathrm{n}} } ^{\mathrm{3}} \right)^{\frac{\mathrm{1}}{\mathrm{n}}} \leqslant\left(\underset{\mathrm{k}=\mathrm{2}} {\overset{\mathrm{n}} {\sum}}\mathrm{sin}\left(\frac{\mathrm{ln}\left(\mathrm{k}\right)}{\mathrm{k}}\right)\right)^{\frac{\mathrm{1}}{\mathrm{n}}} \leqslant\left(\underset{\mathrm{k}=\mathrm{2}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{ln}\left(\mathrm{k}\right)}{\mathrm{k}}\right)^{\frac{\mathrm{1}}{\mathrm{n}}} =\mathrm{u}_{\mathrm{n}} \\ $$$$\mathrm{ln}\left(\mathrm{u}_{\mathrm{n}} \right)=\frac{\mathrm{1}}{\mathrm{n}}\mathrm{ln}\left(\underset{\mathrm{k}=\mathrm{2}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{ln}\left(\mathrm{k}\right)}{\mathrm{k}}\right)\leqslant\frac{\mathrm{1}}{\mathrm{n}}\mathrm{ln}\left(\mathrm{nln}\left(\mathrm{n}\right)\right)\rightarrow\mathrm{0} \\ $$$$\mathrm{ln}\left(\mathrm{v}_{\mathrm{n}} \right)=\frac{\mathrm{1}}{\mathrm{n}}\mathrm{ln}\left(\underset{\mathrm{k}\geqslant\mathrm{2}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{ln}\left(\mathrm{k}\right)}{\mathrm{k}}−\frac{\mathrm{1}}{\mathrm{6}}\left(\frac{\mathrm{ln}\left(\mathrm{k}\right)}{\mathrm{k}}\right)^{\mathrm{3}} \right) \\ $$$$\underset{\mathrm{k}\geqslant\mathrm{2}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{ln}\left(\mathrm{k}\right)}{\mathrm{k}}−\frac{\mathrm{1}}{\mathrm{6}}\left(\frac{\mathrm{ln}\left(\mathrm{k}\right)}{\mathrm{k}}\right)^{\mathrm{3}} \geqslant\underset{\mathrm{k}=\mathrm{2}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{5}}{\mathrm{6}}\frac{\mathrm{ln}\left(\mathrm{k}\right)}{\mathrm{k}}…\left(\mathrm{E}\right) \\ $$$$\exists\mathrm{n}\in\mathbb{N}\:\forall\mathrm{n}\geqslant\mathrm{N}\:\underset{\mathrm{k}=\mathrm{2}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{ln}\left(\mathrm{k}\right)}{\mathrm{k}}.\frac{\mathrm{5}}{\mathrm{6}}\geqslant\mathrm{1} \\ $$$$\mathrm{since}\:\underset{\mathrm{k}\geqslant\mathrm{2}} {\sum}\frac{\mathrm{ln}\left(\mathrm{k}\right)}{\mathrm{k}}\:\mathrm{diverge}\:\mathrm{in}\:+\infty \\ $$$$\mathrm{E}\Rightarrow\underset{\mathrm{k}\geqslant\mathrm{2}} {\overset{\mathrm{n}} {\sum}}\left(\frac{\mathrm{ln}\left(\mathrm{k}\right)}{\mathrm{k}}−\frac{\mathrm{1}}{\mathrm{6}}\left(\frac{\mathrm{ln}\left(\mathrm{k}\right)}{\mathrm{k}}\right)^{\mathrm{3}} \right)\geqslant\mathrm{1},\forall\mathrm{n}\geqslant\mathrm{N} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{n}}\mathrm{ln}\left(\underset{\mathrm{k}\geqslant\mathrm{2}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{lnk}}{\mathrm{k}}−\frac{\mathrm{1}}{\mathrm{6}}\left(\frac{\mathrm{lnk}}{\mathrm{k}}\right)^{\mathrm{3}} \right)\geqslant\mathrm{0},\forall\mathrm{n}\geqslant\mathrm{N} \\ $$$$\Rightarrow\forall\mathrm{n}\geqslant\mathrm{N} \\ $$$$ \\ $$$$\mathrm{0}\leqslant\frac{\mathrm{1}}{\mathrm{n}}\mathrm{ln}\left(\Sigma\mathrm{sin}\left(\frac{\mathrm{lnk}}{\mathrm{k}}\right)\right)^{} \leqslant\mathrm{ln}\left(\mathrm{u}_{\mathrm{n}} \right)\rightarrow\mathrm{0} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{n}}\mathrm{ln}\left(\Sigma\mathrm{sin}\left(\frac{\mathrm{ln}\left(\mathrm{k}\right)}{\mathrm{k}}\right)\right)\rightarrow\mathrm{0} \\ $$$$\Leftrightarrow\left(\underset{\mathrm{k}\geqslant\mathrm{2}} {\sum}\mathrm{sin}\left(\frac{\mathrm{ln}\left(\mathrm{k}\right)}{\mathrm{k}}\right)\right)^{\frac{\mathrm{1}}{\mathrm{n}}} \rightarrow\mathrm{1} \\ $$
Commented by Mingma last updated on 19/Nov/23
Perfect ��

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *