Question Number 200821 by Calculusboy last updated on 24/Nov/23
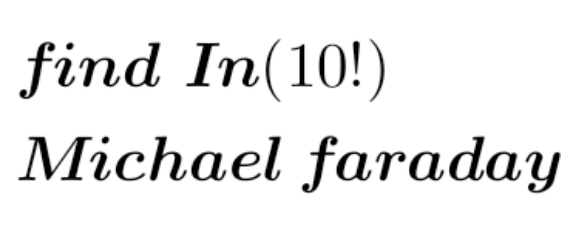
Answered by shunmisaki007 last updated on 24/Nov/23

$$\mathrm{ln}\left(\mathrm{10}!\right) \\ $$$$=\mathrm{ln}\left(\mathrm{10}\centerdot\mathrm{9}\centerdot\mathrm{8}\centerdot\mathrm{7}\centerdot\mathrm{6}\centerdot\mathrm{5}\centerdot\mathrm{4}\centerdot\mathrm{3}\centerdot\mathrm{2}\centerdot\mathrm{1}\right) \\ $$$$=\mathrm{ln}\left(\left(\mathrm{2}\centerdot\mathrm{5}\right)\centerdot\mathrm{3}^{\mathrm{2}} \centerdot\mathrm{2}^{\mathrm{3}} \centerdot\mathrm{7}\centerdot\left(\mathrm{2}\centerdot\mathrm{3}\right)\centerdot\mathrm{5}\centerdot\mathrm{2}^{\mathrm{2}} \centerdot\mathrm{3}\centerdot\mathrm{2}\centerdot\mathrm{1}\right) \\ $$$$=\mathrm{ln}\left(\mathrm{2}^{\mathrm{8}} \centerdot\mathrm{3}^{\mathrm{4}} \centerdot\mathrm{5}^{\mathrm{2}} \centerdot\mathrm{7}\right) \\ $$$$=\mathrm{8ln}\left(\mathrm{2}\right)+\mathrm{4ln}\left(\mathrm{3}\right)+\mathrm{2ln}\left(\mathrm{5}\right)+\mathrm{ln}\left(\mathrm{7}\right)\:…\bigstar \\ $$
Commented by Calculusboy last updated on 26/Nov/23

$$\boldsymbol{{thanks}}\:\boldsymbol{{sir}} \\ $$
Commented by Calculusboy last updated on 26/Nov/23

$$ \\ $$
