Question Number 201223 by Calculusboy last updated on 02/Dec/23
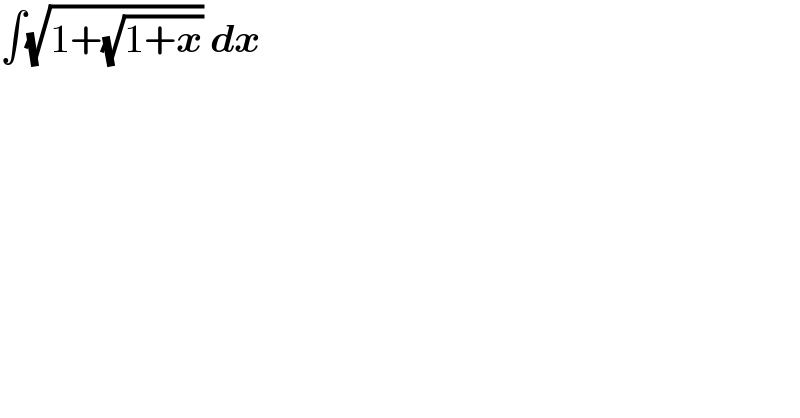
$$\int\sqrt{\mathrm{1}+\sqrt{\mathrm{1}+\boldsymbol{{x}}}}\:\boldsymbol{{dx}} \\ $$
Answered by witcher3 last updated on 02/Dec/23
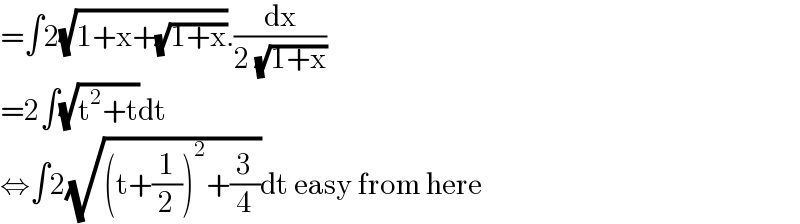
$$=\int\mathrm{2}\sqrt{\mathrm{1}+\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{x}}}.\frac{\mathrm{dx}}{\mathrm{2}\:\sqrt{\mathrm{1}+\mathrm{x}}} \\ $$$$=\mathrm{2}\int\sqrt{\mathrm{t}^{\mathrm{2}} +\mathrm{t}}\mathrm{dt} \\ $$$$\Leftrightarrow\int\mathrm{2}\sqrt{\left(\mathrm{t}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}}\mathrm{dt}\:\mathrm{easy}\:\mathrm{from}\:\mathrm{here} \\ $$
Commented by Calculusboy last updated on 02/Dec/23

$$\boldsymbol{{yes}}\:\boldsymbol{{sir}} \\ $$
