Question Number 202771 by ali009 last updated on 03/Jan/24
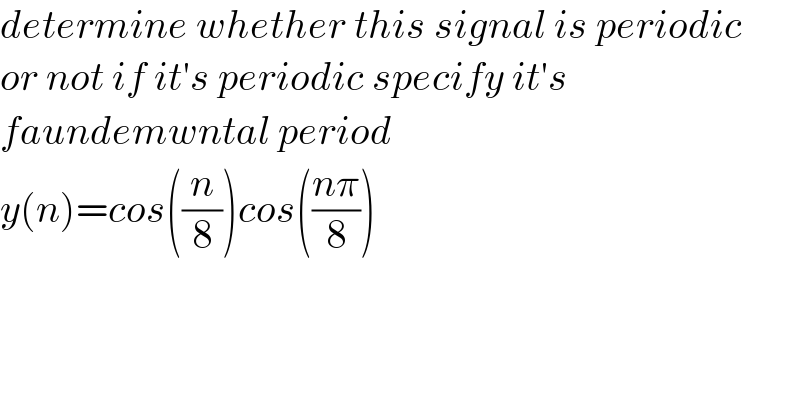
$${determine}\:{whether}\:{this}\:{signal}\:{is}\:{periodic} \\ $$$${or}\:{not}\:{if}\:{it}'{s}\:{periodic}\:{specify}\:{it}'{s}\: \\ $$$${faundemwntal}\:{period} \\ $$$${y}\left({n}\right)={cos}\left(\frac{{n}}{\mathrm{8}}\right){cos}\left(\frac{{n}\pi}{\mathrm{8}}\right)\: \\ $$
Answered by Frix last updated on 03/Jan/24

$$\mathrm{It}'\mathrm{s}\:\mathrm{not}\:\mathrm{periodic}.\:\mathrm{To}\:\mathrm{see}\:\mathrm{what}\:\mathrm{happens}: \\ $$$$\pi\approx\mathrm{3} \\ $$$$\mathrm{cos}\:\frac{{n}}{\mathrm{8}}\:\mathrm{cos}\:\frac{\mathrm{3}{n}}{\mathrm{8}}\:\Rightarrow\:\mathrm{period}\:\mathrm{is}\:\mathrm{8}\pi \\ $$$$\pi\approx\frac{\mathrm{22}}{\mathrm{7}} \\ $$$$\mathrm{cos}\:\frac{{n}}{\mathrm{8}}\:\mathrm{cos}\:\frac{\mathrm{11}{n}}{\mathrm{28}}\:\Rightarrow\:\mathrm{period}\:\mathrm{is}\:\mathrm{112}\pi \\ $$$$\pi\approx\frac{\mathrm{355}}{\mathrm{113}} \\ $$$$\mathrm{cos}\:\frac{{n}}{\mathrm{8}}\:\mathrm{cos}\:\frac{\mathrm{355}{n}}{\mathrm{904}}\:\Rightarrow\:\mathrm{period}\:\mathrm{is}\:\mathrm{904}\pi \\ $$$$… \\ $$$$\mathrm{cos}\:\frac{{n}}{\mathrm{8}}\:\mathrm{cos}\:\frac{{n}\pi}{\mathrm{8}}\:\Rightarrow\:\mathrm{period}\:\mathrm{is}\:\infty \\ $$
