Question Number 202773 by ajfour last updated on 03/Jan/24

Commented by esmaeil last updated on 03/Jan/24

$${only}\:{this}? \\ $$
Commented by mr W last updated on 03/Jan/24

$${only}\:{the}\:{diagonal}\:{of}\:{the}\:{rectangle}\:{is} \\ $$$${defined}.\:{there}\:{is}\:{no}\:{unique}\:{solution} \\ $$$${for}\:{the}\:{area}\:{of}\:{the}\:{rectangle}. \\ $$
Commented by mr W last updated on 03/Jan/24
Commented by mr W last updated on 03/Jan/24

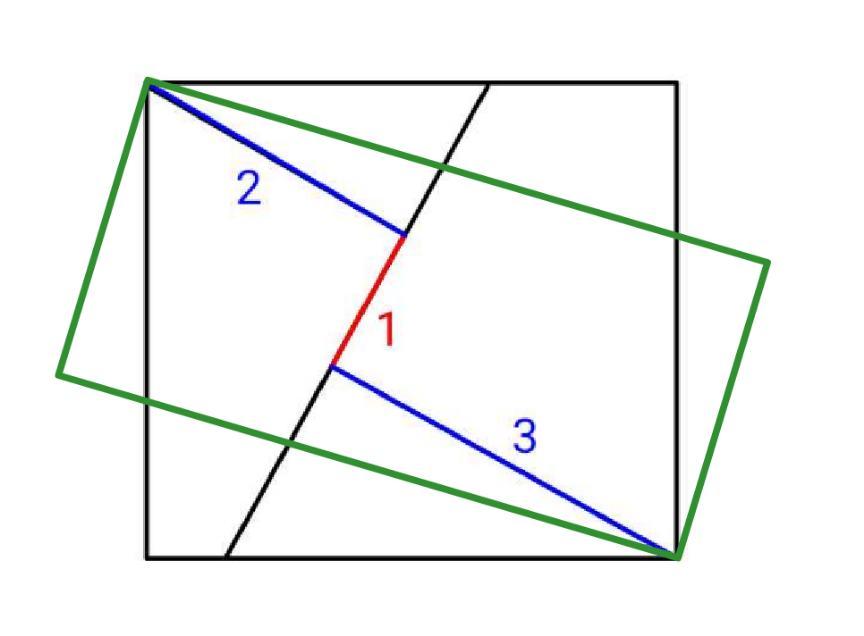
$${then}\:{the}\:{question}\:{is}\:{not}\:{complete}. \\ $$$${with}\:{given}\:{data}\:{we}\:{can}\:{only}\:{say}\:{that} \\ $$$${the}\:{length}\:{of}\:{the}\:{diagonals}\:{is} \\ $$$$\sqrt{\mathrm{1}^{\mathrm{2}} +\left(\mathrm{2}+\mathrm{3}\right)^{\mathrm{2}} }=\sqrt{\mathrm{26}}. \\ $$
Commented by mr W last updated on 03/Jan/24
![the area of the rectangle can be any value in (0, 13].](https://www.tinkutara.com/question/Q202790.png)
$${the}\:{area}\:{of}\:{the}\:{rectangle}\:{can}\:{be} \\ $$$${any}\:{value}\:{in}\:\left(\mathrm{0},\:\mathrm{13}\right]. \\ $$
Commented by ajfour last updated on 03/Jan/24

$${true},\:{agreed},\:{thanks}! \\ $$$${what}\:{if}\:{the}\:{inclined}\:{length}\:{be} \\ $$$${also}\:{given}\:{say}\:{L}=\mathrm{4}\:? \\ $$
Commented by mr W last updated on 03/Jan/24

$${l}=\left(\mathrm{2}+\mathrm{3}\right)\:\mathrm{tan}\:\theta+\mathrm{1}=\mathrm{4} \\ $$$$\Rightarrow\mathrm{tan}\:\theta=\frac{\mathrm{3}}{\mathrm{5}}\Rightarrow\:\mathrm{cos}\:\theta=\frac{\mathrm{5}}{\:\sqrt{\mathrm{34}}},\:\mathrm{sin}\:\theta=\frac{\mathrm{3}}{\:\sqrt{\mathrm{34}}} \\ $$$${a}=\left(\mathrm{2}+\mathrm{3}\right)\:\mathrm{cos}\:\theta−\mathrm{1}\:\mathrm{sin}\:\theta=\frac{\mathrm{22}}{\:\sqrt{\mathrm{34}}} \\ $$$${b}=\left(\mathrm{2}+\mathrm{3}\right)\:\mathrm{sin}\:\theta+\mathrm{1}\:\mathrm{cos}\:\theta=\frac{\mathrm{20}}{\:\sqrt{\mathrm{34}}} \\ $$$${area}\:={ab}=\frac{\mathrm{22}×\mathrm{20}}{\mathrm{34}}\approx\mathrm{12}.\mathrm{94} \\ $$
Commented by ajfour last updated on 03/Jan/24

$${Thank}\:{you}.\:{so}\:{easy}! \\ $$
Commented by mr W last updated on 03/Jan/24

$${yes}\:{sir}! \\ $$
