find-the-seauence-u-n-wich-verify-u-0-1-and-u-n-u-n-1-1-n-n-for-n-1-

Question Number 202865 by Mathspace last updated on 04/Jan/24

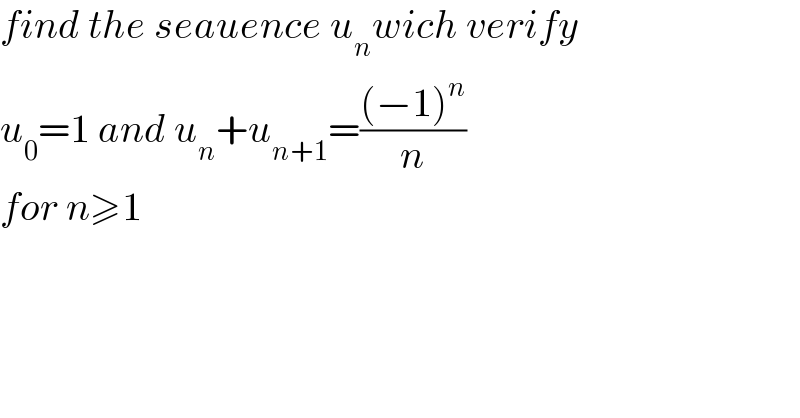
$${find}\:{the}\:{seauence}\:{u}_{{n}} {wich}\:{verify} \\ $$$${u}_{\mathrm{0}} =\mathrm{1}\:{and}\:{u}_{{n}} +{u}_{{n}+\mathrm{1}} =\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}} \\ $$$${for}\:{n}\geqslant\mathrm{1} \\ $$

Commented by mr W last updated on 05/Jan/24

$${you}\:{mean}\:{u}_{\mathrm{1}} =\mathrm{1}? \\ $$

Answered by witcher3 last updated on 04/Jan/24

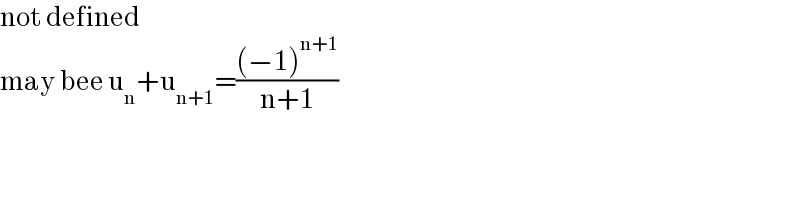
not defined may bee u_n +u_(n+1) =(((−1)^(n+1) )/(n+1))

$$\mathrm{not}\:\mathrm{defined}\: \\ $$$$\mathrm{may}\:\mathrm{bee}\:\mathrm{u}_{\mathrm{n}} +\mathrm{u}_{\mathrm{n}+\mathrm{1}} =\frac{\left(−\mathrm{1}\right)^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}} \\ $$$$ \\ $$

Commented by Mathspace last updated on 05/Jan/24

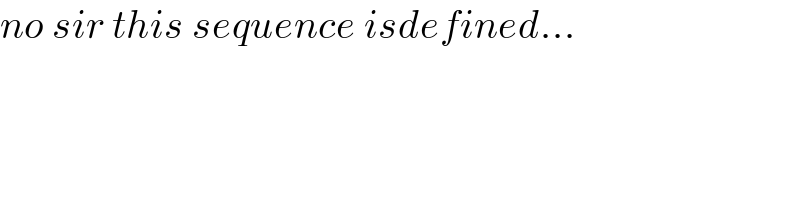
$${no}\:{sir}\:{this}\:{sequence}\:{isdefined}… \\ $$

Answered by Mathspace last updated on 05/Jan/24

$${take}\:{u}_{\mathrm{1}} =\mathrm{1} \\ $$

Answered by witcher3 last updated on 05/Jan/24

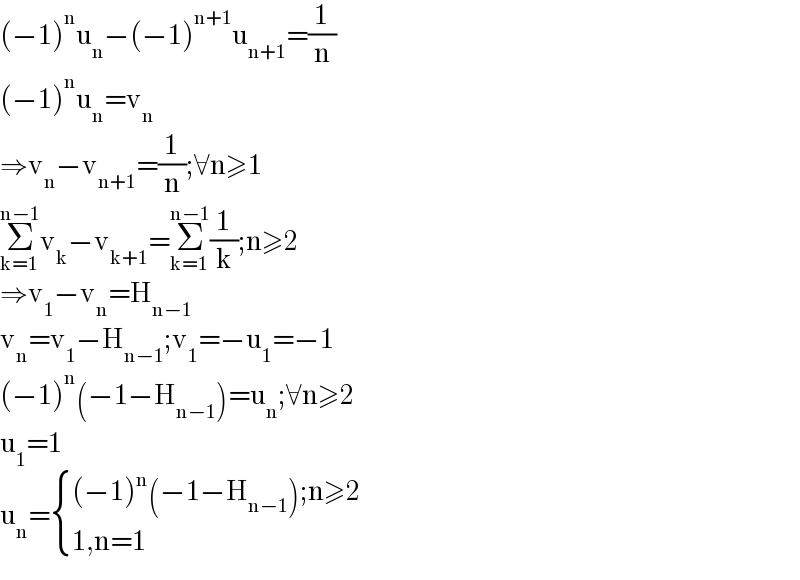
(−1)^n u_n −(−1)^(n+1) u_(n+1) =(1/n) (−1)^n u_n =v_n ⇒v_n −v_(n+1) =(1/n);∀n≥1 Σ_(k=1) ^(n−1) v_k −v_(k+1) =Σ_(k=1) ^(n−1) (1/k);n≥2 ⇒v_1 −v_n =H_(n−1) v_n =v_1 −H_(n−1) ;v_1 =−u_1 =−1 (−1)^n (−1−H_(n−1) )=u_n ;∀n≥2 u_1 =1 u_n = { (((−1)^n (−1−H_(n−1) );n≥2)),((1,n=1)) :}

$$\left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{u}_{\mathrm{n}} −\left(−\mathrm{1}\right)^{\mathrm{n}+\mathrm{1}} \mathrm{u}_{\mathrm{n}+\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{n}} \\ $$$$\left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{u}_{\mathrm{n}} =\mathrm{v}_{\mathrm{n}} \\ $$$$\Rightarrow\mathrm{v}_{\mathrm{n}} −\mathrm{v}_{\mathrm{n}+\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{n}};\forall\mathrm{n}\geqslant\mathrm{1} \\ $$$$\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}−\mathrm{1}} {\sum}}\mathrm{v}_{\mathrm{k}} −\mathrm{v}_{\mathrm{k}+\mathrm{1}} =\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}−\mathrm{1}} {\sum}}\frac{\mathrm{1}}{\mathrm{k}};\mathrm{n}\geqslant\mathrm{2} \\ $$$$\Rightarrow\mathrm{v}_{\mathrm{1}} −\mathrm{v}_{\mathrm{n}} =\mathrm{H}_{\mathrm{n}−\mathrm{1}} \\ $$$$\mathrm{v}_{\mathrm{n}} =\mathrm{v}_{\mathrm{1}} −\mathrm{H}_{\mathrm{n}−\mathrm{1}} ;\mathrm{v}_{\mathrm{1}} =−\mathrm{u}_{\mathrm{1}} =−\mathrm{1} \\ $$$$\left(−\mathrm{1}\right)^{\mathrm{n}} \left(−\mathrm{1}−\mathrm{H}_{\mathrm{n}−\mathrm{1}} \right)=\mathrm{u}_{\mathrm{n}} ;\forall\mathrm{n}\geqslant\mathrm{2} \\ $$$$\mathrm{u}_{\mathrm{1}} =\mathrm{1} \\ $$$$\mathrm{u}_{\mathrm{n}} =\begin{cases}{\left(−\mathrm{1}\right)^{\mathrm{n}} \left(−\mathrm{1}−\mathrm{H}_{\mathrm{n}−\mathrm{1}} \right);\mathrm{n}\geqslant\mathrm{2}}\\{\mathrm{1},\mathrm{n}=\mathrm{1}}\end{cases} \\ $$

Facebook Tweet Pin

find-the-seauence-u-n-wich-verify-u-0-1-and-u-n-u-n-1-1-n-n-for-n-1-

Leave a Reply Cancel reply