Question Number 203291 by zahaku last updated on 14/Jan/24
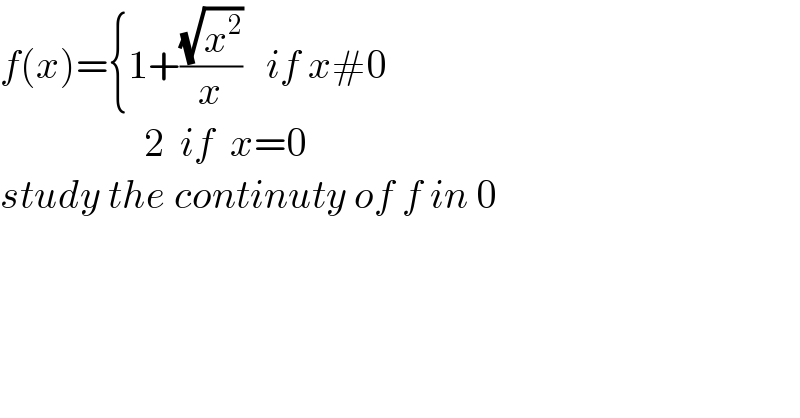
$${f}\left({x}\right)=\left\{\mathrm{1}+\frac{\sqrt{{x}^{\mathrm{2}} }}{{x}}\:\:\:{if}\:{x}#\mathrm{0}\right. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}\:\:{if}\:\:{x}=\mathrm{0} \\ $$$${study}\:{the}\:{continuty}\:{of}\:{f}\:{in}\:\mathrm{0} \\ $$
Answered by esmaeil last updated on 15/Jan/24
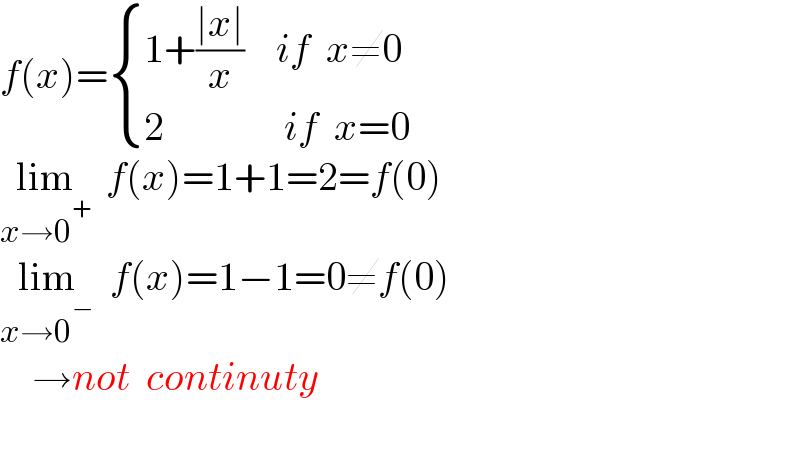
$${f}\left({x}\right)=\begin{cases}{\mathrm{1}+\frac{\mid{x}\mid}{{x}}\:\:\:\:{if}\:\:{x}\neq\mathrm{0}}\\{\mathrm{2}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{if}\:\:{x}=\mathrm{0}}\end{cases}\:\:\: \\ $$$$\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\:{f}\left({x}\right)=\mathrm{1}+\mathrm{1}=\mathrm{2}={f}\left(\mathrm{0}\right) \\ $$$$\underset{{x}\rightarrow\mathrm{0}^{−} } {\mathrm{lim}}\:\:{f}\left({x}\right)=\mathrm{1}−\mathrm{1}=\mathrm{0}\neq{f}\left(\mathrm{0}\right) \\ $$$$\:\:\:\:\rightarrow{not}\:\:{continuty} \\ $$$$ \\ $$
