Question Number 203826 by necx122 last updated on 29/Jan/24
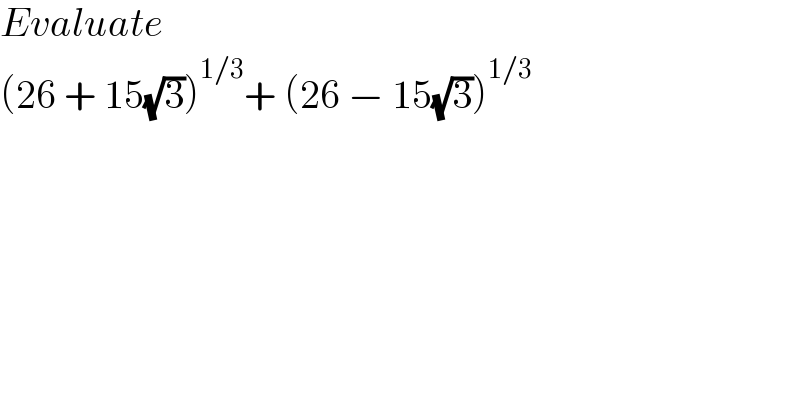
$${Evaluate} \\ $$$$\left(\mathrm{26}\:+\:\mathrm{15}\sqrt{\mathrm{3}}\right)^{\mathrm{1}/\mathrm{3}} +\:\left(\mathrm{26}\:−\:\mathrm{15}\sqrt{\mathrm{3}}\right)^{\mathrm{1}/\mathrm{3}} \\ $$
Answered by AST last updated on 29/Jan/24
![Let a=((26+15(√3)))^(1/3) ;b=((26−15(√3)))^(1/3) ⇒ab=1 a^3 +b^3 =52=(a+b)^3 −3ab(a+b)=(a+b)[(a+b)^2 −3] x^3 −3x−52=0⇒x=4=a+b=((26+15(√3)))^(1/3) +((26−15(√3)))^(1/3)](https://www.tinkutara.com/question/Q203827.png)
$${Let}\:{a}=\sqrt[{\mathrm{3}}]{\mathrm{26}+\mathrm{15}\sqrt{\mathrm{3}}};{b}=\sqrt[{\mathrm{3}}]{\mathrm{26}−\mathrm{15}\sqrt{\mathrm{3}}}\Rightarrow{ab}=\mathrm{1} \\ $$$${a}^{\mathrm{3}} +{b}^{\mathrm{3}} =\mathrm{52}=\left({a}+{b}\right)^{\mathrm{3}} −\mathrm{3}{ab}\left({a}+{b}\right)=\left({a}+{b}\right)\left[\left({a}+{b}\right)^{\mathrm{2}} −\mathrm{3}\right] \\ $$$${x}^{\mathrm{3}} −\mathrm{3}{x}−\mathrm{52}=\mathrm{0}\Rightarrow{x}=\mathrm{4}={a}+{b}=\sqrt[{\mathrm{3}}]{\mathrm{26}+\mathrm{15}\sqrt{\mathrm{3}}}+\sqrt[{\mathrm{3}}]{\mathrm{26}−\mathrm{15}\sqrt{\mathrm{3}}} \\ $$
Answered by esmaeil last updated on 29/Jan/24

$$=\Omega \\ $$$${way}\:\mathrm{2} \\ $$$$\left(\mathrm{26}+\mathrm{15}\sqrt{\mathrm{3}}\right)=\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\mathrm{3}} \\ $$$$\left(\mathrm{26}−\mathrm{15}\sqrt{\mathrm{3}}\right)=\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)^{\mathrm{3}} \rightarrow \\ $$$$\Omega=\mathrm{4} \\ $$
Answered by Rasheed.Sindhi last updated on 30/Jan/24

$$\left(\underset{{a}} {\underbrace{\mathrm{26}\:+\:\mathrm{15}\sqrt{\mathrm{3}}}}\right)^{\mathrm{1}/\mathrm{3}} +\:\left(\underset{{b}} {\underbrace{\mathrm{26}\:−\:\mathrm{15}\sqrt{\mathrm{3}}}}\right)^{\mathrm{1}/\mathrm{3}} \\ $$$${a}^{\mathrm{1}/\mathrm{3}} +\:{b}^{\mathrm{1}/\mathrm{3}} ={p}\:\:\left({say}\right)….\left({i}\right) \\ $$$${a}^{\mathrm{2}/\mathrm{3}} +\:{b}^{\mathrm{2}/\mathrm{3}} +\mathrm{2}{a}^{\mathrm{1}/\mathrm{3}} {b}^{\mathrm{1}/\mathrm{3}} ={p}^{\mathrm{2}} \:\:\left({say}\right) \\ $$$$\because\:{a}^{\mathrm{1}/\mathrm{3}} {b}^{\mathrm{1}/\mathrm{3}} =\left({ab}\right)^{\mathrm{1}/\mathrm{3}} =\mathrm{1}^{\mathrm{1}/\mathrm{3}} =\mathrm{1} \\ $$$$\therefore\:{a}^{\mathrm{2}/\mathrm{3}} +\:{b}^{\mathrm{2}/\mathrm{3}} ={p}^{\mathrm{2}} −\mathrm{2}……\left({ii}\right) \\ $$$$\left({i}\right)×\left({ii}\right): \\ $$$${a}+{b}+{a}^{\mathrm{1}/\mathrm{3}} {b}^{\mathrm{1}/\mathrm{3}} \left({a}^{\mathrm{1}/\mathrm{3}} +\:{b}^{\mathrm{1}/\mathrm{3}} \right)={p}^{\mathrm{3}} −\mathrm{2}{p} \\ $$$${a}+{b}+\left(\mathrm{1}\right)\left({p}\right)={p}^{\mathrm{3}} −\mathrm{2}{p} \\ $$$${p}^{\mathrm{3}} −\mathrm{3}{p}={a}+{b}=\mathrm{26}+\mathrm{15}\sqrt{\mathrm{3}}\:+\mathrm{26}−\mathrm{15}\sqrt{\mathrm{3}}\:=\mathrm{52} \\ $$$${p}^{\mathrm{3}} −\mathrm{3}{p}−\mathrm{52}=\mathrm{0}\Rightarrow{p}=\mathrm{4} \\ $$$$\: \\ $$
Commented by necx122 last updated on 30/Jan/24
Thank you so so much sir. This too is wonderful.
