How-many-bit-strings-of-length-10-do-not-have-four-consecutive-1s-

Question Number 203832 by depressiveshrek last updated on 29/Jan/24

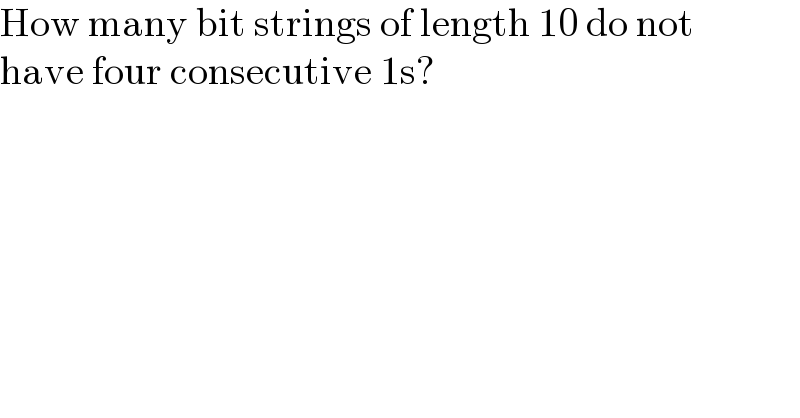
How many bit strings of length 10 do not

have four consecutive 1 s ?

Answered by nikif99 last updated on 30/Jan/24

T o t a l n u m b e r o f b i t s t r i n g s o f l e n g t h 10

i s 2^{10} = 1024 (0 - 1023) .

O f t h e m, t h e r e a r e 7 b i t s t r i n g s o f

e x a c t l y 4^{'} 1^{'} s a t p o s i h i o n s 1 - 7 .

00 \underset{}{\underset{⏟}{1111} 0000}

F u r t h e r m o r e, t h e r e a r e 3 b i t s t r i n g s

o f m o r e t h a n o n e^{'} 1111^{'} :

1111011110

1111001111

0111101111

A n s w e r : 1024 - 7 - 3 = 1014

Commented by AST last updated on 30/Jan/24

I t s e e m s 1011110000, 1110111100, e t c s h o u l d

a l s o b e v a l i d f o r t h o s e c o n t a i n i n g t h e s t r i n g

1111

Commented by nikif99 last updated on 30/Jan/24

Y o u a r e r i g h t . I s h o u l d r e - e x a m i n e i t .

T h a n k y o u .

Commented by nikif99 last updated on 30/Jan/24

R e - e v a l u a t i n g m y c o m p u t a t i o n s :

I n a 10 - b i t s t r i n g, I f i x a s e r i e s o f

4 c o n s e c u t i v e^{'} 1^{'} s e n s u r i n g a d j a c e n t

b i t s (i f e x i x t) a r e s e t t o 0 . E x a m p l e :

0011110000 w h e r e

r e d s a r e s e t t o 1, b l u e s a r e s e t t o 0 t o

p r o h i b i t e x p a n s i o n o f r e d s a n d b l a c k s

d e r i v e a 4 - b i t s e t w i t h v a l u e s 0 t o 15 .

S o, w e h a v e n e x t o p t i o n s .

a) 11110 \underset{}{\underset{⏟}{00000}} (32 c a s e s)

b) 011110 \underset{}{\underset{⏟}{0000}} (16)

c) 0011110000 (16)

d) 0001111000 (16)

e) 0000111100 (16)

f) 0000011110 (16)

g) 0000001111 (32)

t o t a l 32 \times 2 + 16 \times 5 = 144

m i n u s 2 f o r 0111101111 a n d 1111001111

w h i c h a r e d o u b l e c o u n t e d = 142 w i t h 4

c o n c e c u t i v e^{'} 1^{'} s .

N o n c o n s e c u t i v e o n e s a r e

1024 - 142 = 882

Commented by AST last updated on 31/Jan/24

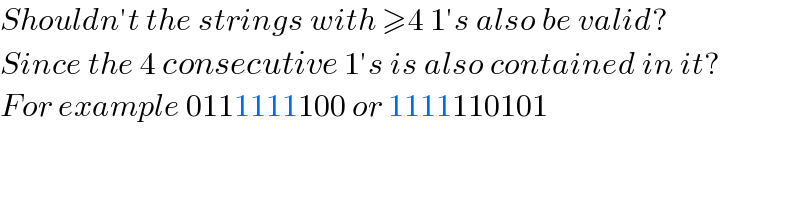
{S h o u l d n}^{'} t t h e s t r i n g s w i t h ⩾ 4 1^{'} s a l s o b e v a l i d ?

S i n c e t h e 4 c o n s e c u t i v e 1^{'} s i s a l s o c o n t a i n e d i n i t ?

F o r e x a m p l e 0111111100 o r 1111110101

Commented by nikif99 last updated on 30/Jan/24

T h e q u e s t i o n i s “ d o n o t h a v e 4

c o n s e c u h i v e 1 s^{″}, 0111111100 h a s 7,

s o I c o n s i d e r i s n o t c o n t a i n e d .

{T h a t}^{'} s w h y I b l o c k e d n e i g h b o u r i n g

p l a c e s w i t h 0 .

Commented by AST last updated on 30/Jan/24

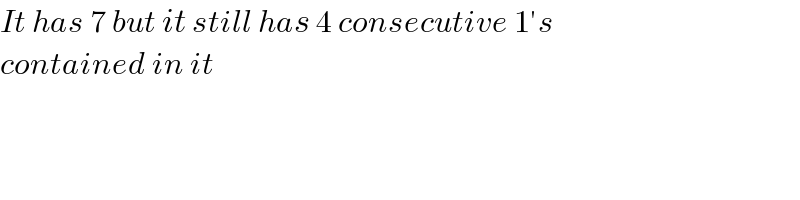
I t h a s 7 b u t i t s t i l l h a s 4 c o n s e c u t i v e 1^{'} s

c o n t a i n e d i n i t

Answered by AST last updated on 31/Jan/24

C a s e 1 : 1111______\Rightarrow 2^{6} w a y s

C a s e 2 :__{1} 1111_____\Rightarrow 2^{5} \times 1 w a y s a n d__{1} = 0

C a s e 3 :__{1}__{2} 1111____

P o s s i b l e f o r (__{1},__{2}) = (1, 1), (1, 0), (0, 1), (0, 0)

O f t h i s, o n l y (1, 0) \land (0, 0) {h a v e n}^{'} t b e e n a c c o u n t e d

You can't use 'macro parameter character #' in math mode

C a s e 4 :__{1}__{2}__{3} 1111___

P o s s i b l e : (0, 0, 0), (0, 0, 1), (0, 1, 0), (1, 0, 0), (0, 1, 1)

(1, 0, 1), (1, 1, 0)

You can't use 'macro parameter character #' in math mode

C a s e 5 :__{1}__{2}__{3}__{4} 1111__\Rightarrow 2^{3} \times 2^{2} = 2^{5} w a y s

C a s e 6 :__{1}__{2}__{3}__{4}__{5} 1111_

O t h e r t h a n c a s e 1,__{5} a l w a y s c o n t a i n e d 1

You can't use 'macro parameter character #' in math mode

C a s e 7 :__{1}__{2}__{3}__{4}__{5}__{6} 1111

__{6} = 0 a n d__{1}__{2}__{3}__{4}__{5} i s s u c h t h a t i t c o n t a i n s n o

4 c o n s e c u t i v e 1^{'} s (11110, 01111, 11111)

You can't use 'macro parameter character #' in math mode

You can't use 'macro parameter character #' in math mode

You can't use 'macro parameter character #' in math mode

= 773

Commented by nikif99 last updated on 31/Jan/24

G o o d a n d c l e a r e x p l a n a t i o n .

Facebook Tweet Pin