Question Number 203905 by sniper237 last updated on 01/Feb/24
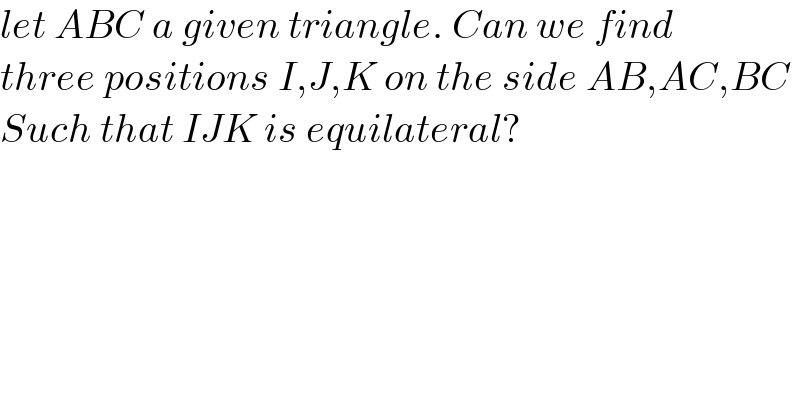
Commented by mr W last updated on 01/Feb/24
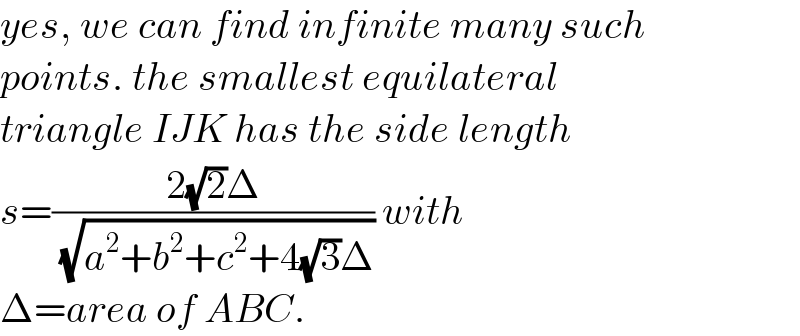
Commented by mr W last updated on 01/Feb/24
Commented by mr W last updated on 01/Feb/24
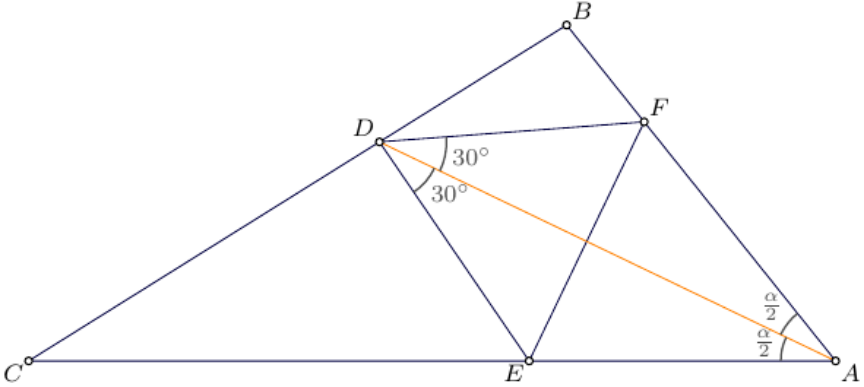
Commented by Rasheed.Sindhi last updated on 02/Feb/24
Commented by mr W last updated on 03/Feb/24

Commented by mr W last updated on 03/Feb/24
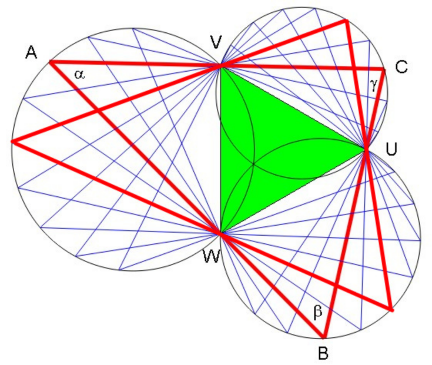
Commented by mr W last updated on 02/Feb/24
Commented by Rasheed.Sindhi last updated on 03/Feb/24