Question Number 205045 by cortano12 last updated on 06/Mar/24

$$\:\:\:\:\underbrace{ \underline{}\:} \\ $$
Commented by Rasheed.Sindhi last updated on 06/Mar/24
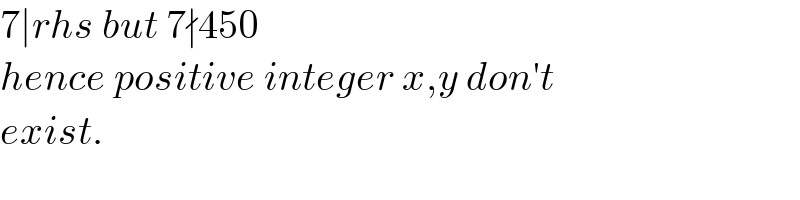
$$\mathrm{7}\mid{rhs}\:{but}\:\mathrm{7}\nmid\mathrm{450} \\ $$$${hence}\:{positive}\:{integer}\:{x},{y}\:{don}'{t} \\ $$$${exist}. \\ $$
Commented by cortano12 last updated on 06/Mar/24

$$\mathrm{how}\:\mathrm{about}\:\mathrm{if}\:\mathrm{2x}+\mathrm{3y}\:=\:\mathrm{450}\: \\ $$$$\:\left(\mathrm{x}+\mathrm{y}\right)_{\mathrm{max}} \:\mathrm{for}\:\mathrm{x},\mathrm{y}\:\in\mathrm{Z}^{+} \\ $$
Commented by Rasheed.Sindhi last updated on 06/Mar/24
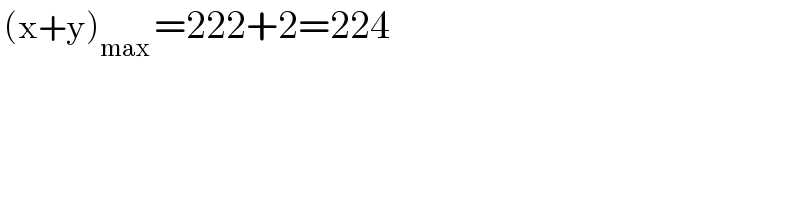
$$\:\left(\mathrm{x}+\mathrm{y}\right)_{\mathrm{max}} \:=\mathrm{222}+\mathrm{2}=\mathrm{224} \\ $$
Commented by A5T last updated on 06/Mar/24
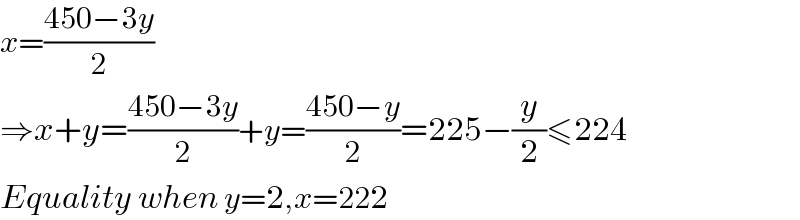
$${x}=\frac{\mathrm{450}−\mathrm{3}{y}}{\mathrm{2}} \\ $$$$\Rightarrow{x}+{y}=\frac{\mathrm{450}−\mathrm{3}{y}}{\mathrm{2}}+{y}=\frac{\mathrm{450}−{y}}{\mathrm{2}}=\mathrm{225}−\frac{{y}}{\mathrm{2}}\leqslant\mathrm{224} \\ $$$${Equality}\:{when}\:{y}=\mathrm{2},{x}=\mathrm{222} \\ $$
