Question Number 205262 by mathzup last updated on 13/Mar/24
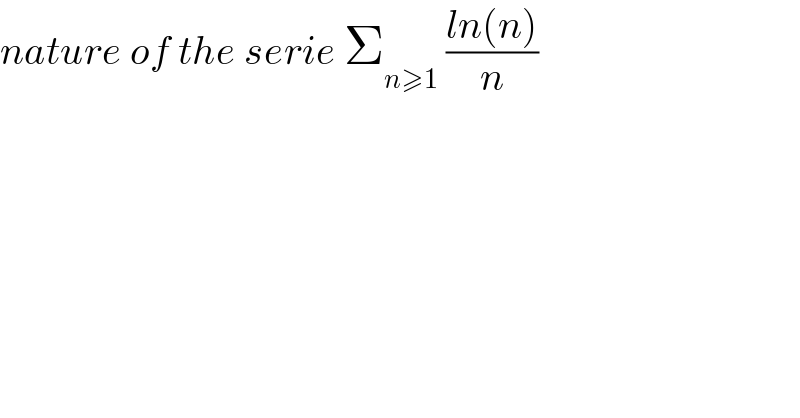
$${nature}\:{of}\:{the}\:{serie}\:\sum_{{n}\geqslant\mathrm{1}} \:\frac{{ln}\left({n}\right)}{{n}} \\ $$
Answered by Berbere last updated on 13/Mar/24
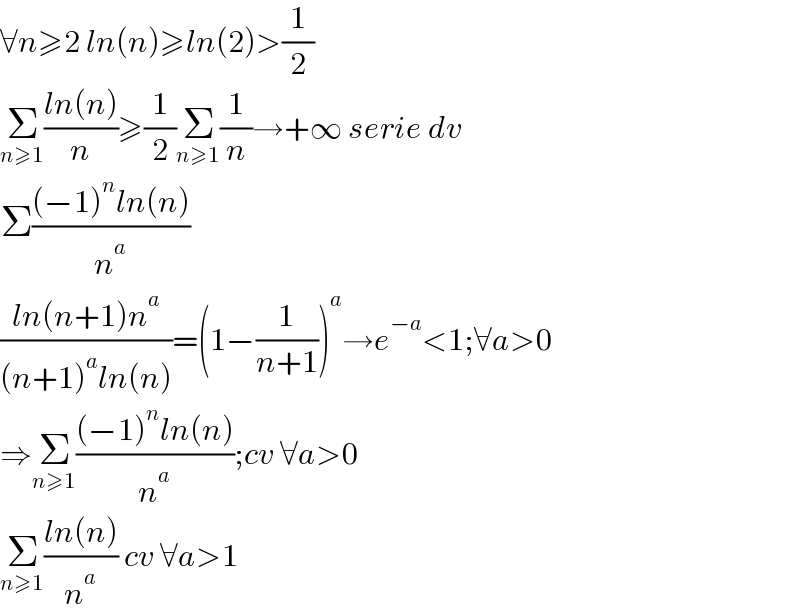
$$\forall{n}\geqslant\mathrm{2}\:{ln}\left({n}\right)\geqslant{ln}\left(\mathrm{2}\right)>\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{{ln}\left({n}\right)}{{n}}\geqslant\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{{n}}\rightarrow+\infty\:{serie}\:{dv} \\ $$$$\Sigma\frac{\left(−\mathrm{1}\right)^{{n}} {ln}\left({n}\right)}{{n}^{{a}} } \\ $$$$\frac{{ln}\left({n}+\mathrm{1}\right){n}^{{a}} }{\left({n}+\mathrm{1}\right)^{{a}} {ln}\left({n}\right)}=\left(\mathrm{1}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\right)^{{a}} \rightarrow{e}^{−{a}} <\mathrm{1};\forall{a}>\mathrm{0} \\ $$$$\Rightarrow\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}} {ln}\left({n}\right)}{{n}^{{a}} };{cv}\:\forall{a}>\mathrm{0} \\ $$$$\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{{ln}\left({n}\right)}{{n}^{{a}} }\:{cv}\:\forall{a}>\mathrm{1} \\ $$
