Question Number 205403 by BaliramKumar last updated on 20/Mar/24
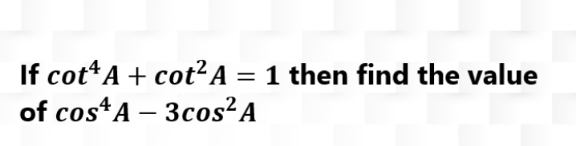
Answered by Rajpurohith last updated on 20/Mar/24

$${Clearly}\:\mathrm{cot}^{\mathrm{2}} \left({A}\right)\left(\mathrm{1}+\mathrm{cot}^{\mathrm{2}} \left({A}\right)\right)=\mathrm{1} \\ $$$${i}.{e},\mathrm{cot}^{\mathrm{2}} \left({A}\right)\left(\mathrm{cosec}^{\mathrm{2}} \left({A}\right)\right)=\mathrm{1} \\ $$$$\Rightarrow\frac{\mathrm{cos}^{\mathrm{2}} \left({A}\right)}{\mathrm{sin}^{\mathrm{4}} \left({A}\right)}=\mathrm{1} \\ $$$$\:{or}\:\mathrm{cos}^{\mathrm{2}} \left({A}\right)=\mathrm{sin}^{\mathrm{4}} \left({A}\right)=\left(\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \left({A}\right)\right)^{\mathrm{2}} \\ $$$${or}\:{cos}^{\mathrm{2}} \left({A}\right)=\mathrm{1}+\mathrm{cos}^{\mathrm{4}} \left({A}\right)−\mathrm{2}{cos}^{\mathrm{2}} \left({A}\right) \\ $$$$\Rightarrow{cos}^{\mathrm{4}} \left({A}\right)−\mathrm{3}{cos}^{\mathrm{2}} \left({A}\right)=−\mathrm{1} \\ $$$$ \\ $$
Commented by BaliramKumar last updated on 20/Mar/24

$$\mathrm{thanks} \\ $$
