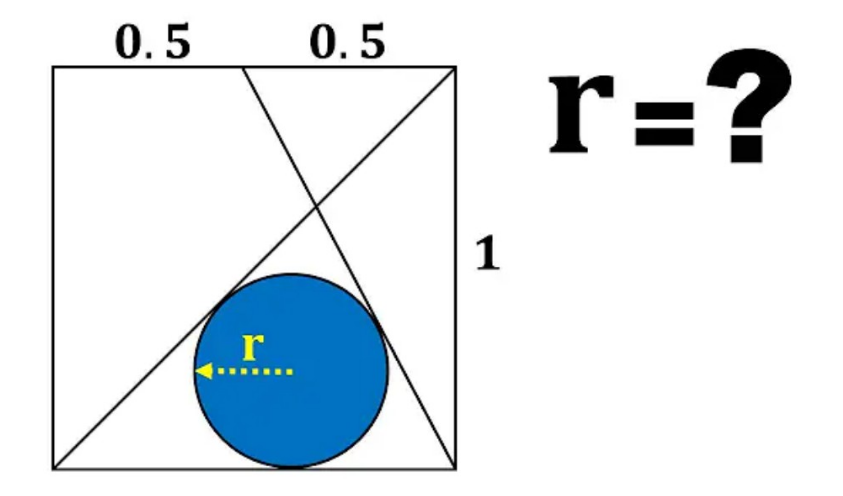
Question Number 205614 by mr W last updated on 25/Mar/24
Answered by A5T last updated on 25/Mar/24

Commented by A5T last updated on 25/Mar/24

$$\frac{{sin}\left(\angle{CFB}\right)}{\mathrm{1}}=\frac{{sin}\mathrm{90}=\mathrm{1}}{\:\sqrt{\mathrm{0}.\mathrm{5}^{\mathrm{2}} +\mathrm{1}}}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\Rightarrow{cos}\left(\angle{CFB}\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}} \\ $$$${sin}\left({FEC}\right)={sin}\left(\mathrm{135}−\angle{CFB}\right)=\frac{\mathrm{3}\sqrt{\mathrm{10}}}{\mathrm{10}} \\ $$$$\frac{{sin}\left({FEC}\right)}{\mathrm{0}.\mathrm{5}}=\frac{{sin}\left({EFC}\right)}{{CE}}\Rightarrow{CE}=\frac{\sqrt{\mathrm{2}}}{\mathrm{3}} \\ $$$${FE}=\sqrt{\mathrm{0}.\mathrm{5}^{\mathrm{2}} +\frac{\mathrm{2}}{\mathrm{9}}−\frac{\mathrm{1}}{\mathrm{3}}}=\frac{\sqrt{\mathrm{5}}}{\mathrm{6}} \\ $$$$\Rightarrow{AE}=\sqrt{\mathrm{2}}−\frac{\sqrt{\mathrm{2}}}{\mathrm{3}}=\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}};{BE}=\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}−\frac{\sqrt{\mathrm{5}}}{\mathrm{6}}=\frac{\sqrt{\mathrm{5}}}{\mathrm{3}} \\ $$$${Area}\:{of}\:{AEB}=\frac{{AE}×{EBsinAEB}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\Rightarrow\frac{{r}}{\mathrm{2}}\left(\frac{\sqrt{\mathrm{5}}+\mathrm{2}\sqrt{\mathrm{2}}+\mathrm{3}}{\mathrm{3}}\right)=\frac{\mathrm{1}}{\mathrm{3}}\Rightarrow{r}=\frac{\mathrm{2}}{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}+\sqrt{\mathrm{5}}}\approx\mathrm{0}.\mathrm{248} \\ $$
Commented by mr W last updated on 25/Mar/24
��
Answered by mr W last updated on 25/Mar/24

Commented by mr W last updated on 25/Mar/24
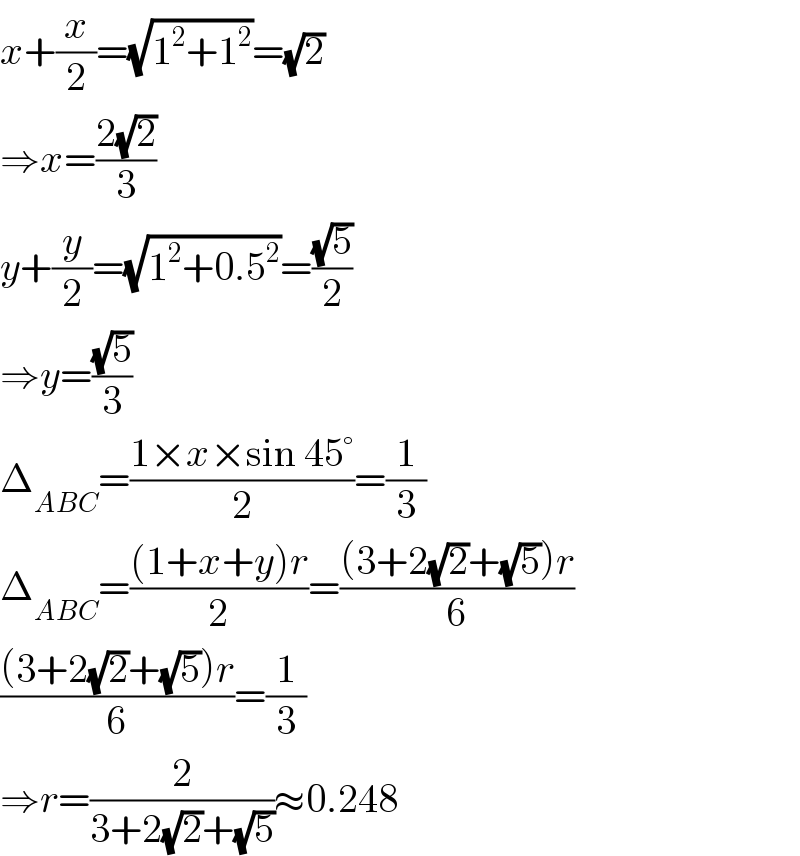
$${x}+\frac{{x}}{\mathrm{2}}=\sqrt{\mathrm{1}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} }=\sqrt{\mathrm{2}} \\ $$$$\Rightarrow{x}=\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}} \\ $$$${y}+\frac{{y}}{\mathrm{2}}=\sqrt{\mathrm{1}^{\mathrm{2}} +\mathrm{0}.\mathrm{5}^{\mathrm{2}} }=\frac{\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\Rightarrow{y}=\frac{\sqrt{\mathrm{5}}}{\mathrm{3}} \\ $$$$\Delta_{{ABC}} =\frac{\mathrm{1}×{x}×\mathrm{sin}\:\mathrm{45}°}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\Delta_{{ABC}} =\frac{\left(\mathrm{1}+{x}+{y}\right){r}}{\mathrm{2}}=\frac{\left(\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}+\sqrt{\mathrm{5}}\right){r}}{\mathrm{6}} \\ $$$$\frac{\left(\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}+\sqrt{\mathrm{5}}\right){r}}{\mathrm{6}}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\Rightarrow{r}=\frac{\mathrm{2}}{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}+\sqrt{\mathrm{5}}}\approx\mathrm{0}.\mathrm{248} \\ $$
