Question Number 205607 by SANOGO last updated on 25/Mar/24
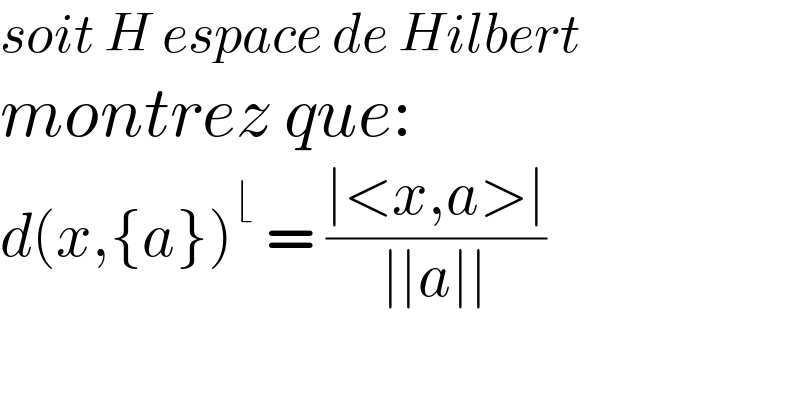
$${soit}\:{H}\:{espace}\:{de}\:{Hilbert} \\ $$$${montrez}\:{que}: \\ $$$${d}\left({x},\left\{{a}\right\}\right)^{\lfloor} \:=\:\frac{\mid<{x},{a}>\mid}{\mid\mid{a}\mid\mid} \\ $$
Answered by Berbere last updated on 25/Mar/24

$$\frac{{a}}{\mid{a}\mid},{a}_{\mathrm{2}} …..{a}_{{n}} \:{une}\:{base}\:{orthonmal} \\ $$$${x}=\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}<{x},\frac{{a}_{{i}} }{\mid{a}\mid}>\frac{{a}_{{i}} }{\mid{a}\mid} \\ $$$${x}=<{x},\frac{{a}}{\mid{a}\mid}>\frac{{a}}{\mid{a}\mid}+{y};{y}\in\left\{{a}\right\}^{\bot} \\ $$$${d}\left({x},\left\{{a}\right\}\right)\mid<{x},\frac{{a}}{\mid{a}\mid}>\mid=\mid\frac{\mathrm{1}}{\mid{a}\mid}<{x},{a}>\mid=\frac{<{x},{a}>}{\mid\mid{a}\mid\mid} \\ $$
Commented by SANOGO last updated on 25/Mar/24
$${thank}\:{you} \\ $$
