Question Number 205645 by hardmath last updated on 26/Mar/24
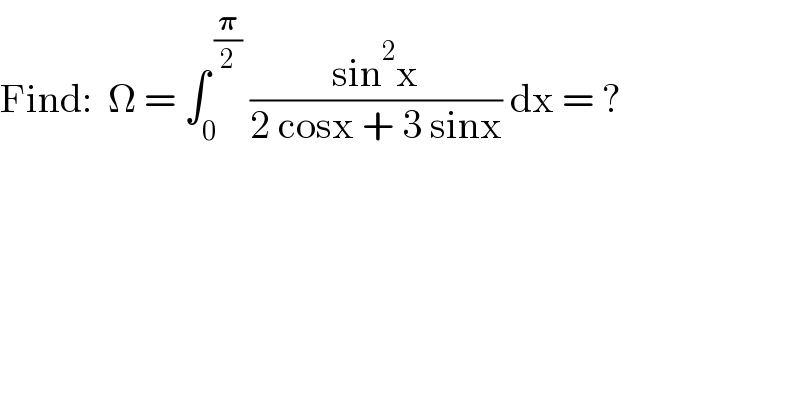
$$\mathrm{Find}:\:\:\Omega\:=\:\int_{\mathrm{0}} ^{\:\frac{\boldsymbol{\pi}}{\mathrm{2}}} \:\frac{\mathrm{sin}^{\mathrm{2}} \mathrm{x}}{\mathrm{2}\:\mathrm{cosx}\:+\:\mathrm{3}\:\mathrm{sinx}}\:\mathrm{dx}\:=\:? \\ $$
Answered by Frix last updated on 26/Mar/24
![t=tan (x/2) leads to â4âŤ(t^2 /((t^2 +1)^2 (t^2 â3tâ1)))dt which can be solved but... I found this: (s^2 /(2c+3s))=((s^2 (2câ3s))/((2c+3s)(2câ3s)))=((3s^3 )/(13s^2 â4))â((2cs^2 )/(13s^2 â4)) â Ί_1 =3âŤ_0 ^(Ď/2) ((sin^3 x)/(13sin^2 x â4))dx =^(u=cos x) 3âŤ_0 ^1 ((u^2 â1)/(13u^2 â9))du= =[((3u)/(13))+((2(â(13)))/(169))ln âŁ(((â(13))u+3)/( (â(13))uâ3))âŁ]_0 ^1 = (3/(13))+((4(â(13)))/(169))(ln 2 âln (â3+(â(13)))) Ί_2 =â2âŤ_0 ^(Ď/2) ((cos x sin^2 x)/(13sin^2 x â4))dx =^(v=sin x) â2âŤ_0 ^1 (v^2 /(13v^2 â4))dv= =[â((2v)/(13))+((2(â(13)))/(169))ln âŁ(((â(13))v+2)/( (â(13))vâ2))âŁ]_0 ^1 = =â(2/(13))+((4(â(13)))/(169))(ln (2+(â(13))) âln 3)) â Ί=(1/(13))+((4(â(13)))/(169))(2ln (5+(â(13))) âln 3 â2ln 2) â.232231309](https://www.tinkutara.com/question/Q205655.png)
$${t}=\mathrm{tan}\:\frac{{x}}{\mathrm{2}}\:\mathrm{leads}\:\mathrm{to} \\ $$$$â\mathrm{4}\int\frac{{t}^{\mathrm{2}} }{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} \left({t}^{\mathrm{2}} â\mathrm{3}{t}â\mathrm{1}\right)}{dt} \\ $$$$\mathrm{which}\:\mathrm{can}\:\mathrm{be}\:\mathrm{solved}\:\mathrm{but}… \\ $$$$\mathrm{I}\:\mathrm{found}\:\mathrm{this}: \\ $$$$\frac{{s}^{\mathrm{2}} }{\mathrm{2}{c}+\mathrm{3}{s}}=\frac{{s}^{\mathrm{2}} \left(\mathrm{2}{c}â\mathrm{3}{s}\right)}{\left(\mathrm{2}{c}+\mathrm{3}{s}\right)\left(\mathrm{2}{c}â\mathrm{3}{s}\right)}=\frac{\mathrm{3}{s}^{\mathrm{3}} }{\mathrm{13}{s}^{\mathrm{2}} â\mathrm{4}}â\frac{\mathrm{2}{cs}^{\mathrm{2}} }{\mathrm{13}{s}^{\mathrm{2}} â\mathrm{4}} \\ $$$$\Rightarrow \\ $$$$\Omega_{\mathrm{1}} =\mathrm{3}\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\frac{\mathrm{sin}^{\mathrm{3}} \:{x}}{\mathrm{13sin}^{\mathrm{2}} \:{x}\:â\mathrm{4}}{dx}\:\overset{{u}=\mathrm{cos}\:{x}} {=}\:\mathrm{3}\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\frac{{u}^{\mathrm{2}} â\mathrm{1}}{\mathrm{13}{u}^{\mathrm{2}} â\mathrm{9}}{du}= \\ $$$$=\left[\frac{\mathrm{3}{u}}{\mathrm{13}}+\frac{\mathrm{2}\sqrt{\mathrm{13}}}{\mathrm{169}}\mathrm{ln}\:\mid\frac{\sqrt{\mathrm{13}}{u}+\mathrm{3}}{\:\sqrt{\mathrm{13}}{u}â\mathrm{3}}\mid\right]_{\mathrm{0}} ^{\mathrm{1}} = \\ $$$$\frac{\mathrm{3}}{\mathrm{13}}+\frac{\mathrm{4}\sqrt{\mathrm{13}}}{\mathrm{169}}\left(\mathrm{ln}\:\mathrm{2}\:â\mathrm{ln}\:\left(â\mathrm{3}+\sqrt{\mathrm{13}}\right)\right) \\ $$$$\Omega_{\mathrm{2}} =â\mathrm{2}\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\frac{\mathrm{cos}\:{x}\:\mathrm{sin}^{\mathrm{2}} \:{x}}{\mathrm{13sin}^{\mathrm{2}} \:{x}\:â\mathrm{4}}{dx}\:\overset{{v}=\mathrm{sin}\:{x}} {=}\:â\mathrm{2}\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\frac{{v}^{\mathrm{2}} }{\mathrm{13}{v}^{\mathrm{2}} â\mathrm{4}}{dv}= \\ $$$$=\left[â\frac{\mathrm{2}{v}}{\mathrm{13}}+\frac{\mathrm{2}\sqrt{\mathrm{13}}}{\mathrm{169}}\mathrm{ln}\:\mid\frac{\sqrt{\mathrm{13}}{v}+\mathrm{2}}{\:\sqrt{\mathrm{13}}{v}â\mathrm{2}}\mid\right]_{\mathrm{0}} ^{\mathrm{1}} = \\ $$$$\left.=â\frac{\mathrm{2}}{\mathrm{13}}+\frac{\mathrm{4}\sqrt{\mathrm{13}}}{\mathrm{169}}\left(\mathrm{ln}\:\left(\mathrm{2}+\sqrt{\mathrm{13}}\right)\:â\mathrm{ln}\:\mathrm{3}\right)\right) \\ $$$$\Rightarrow \\ $$$$\Omega=\frac{\mathrm{1}}{\mathrm{13}}+\frac{\mathrm{4}\sqrt{\mathrm{13}}}{\mathrm{169}}\left(\mathrm{2ln}\:\left(\mathrm{5}+\sqrt{\mathrm{13}}\right)\:â\mathrm{ln}\:\mathrm{3}\:â\mathrm{2ln}\:\mathrm{2}\right) \\ $$$$\approx.\mathrm{232231309} \\ $$