Menu Close

Question-205656

Tinku Tara 0 Comments
Pin




Question Number 205656 by SANOGO last updated on 26/Mar/24
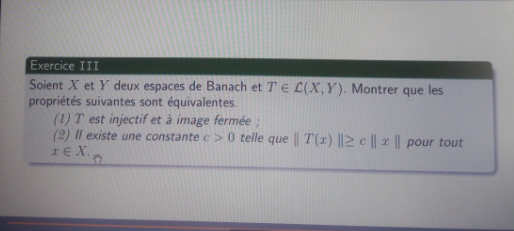
Answered by TheHoneyCat last updated on 31/Mar/24
(2)⇒(1) Soit c∈R^∗ tel que ∀x∈X ∣∣T(x)∣∣_Y ≥c∣∣x∣∣_X Soit (x,x′)∈X^2 ∣∣T(x)−T(x′)∣∣ =∣∣T(x−x′)∣∣ ≥c∣∣x−x′∣∣ T(x)=T(x′) ⇒T(x)−T(x′)=0 ⇒∣∣T(x)−T(x′)∣∣=0 ⇒c∣∣x−x′∣∣=0 ⇒∣∣x−x′∣∣=0 ⇒x−x′=0 ⇒x=x′ Donc (2)⇒ T injectif Soit (t_n ) une suite de Im(X) convergente dans Y. Puisque (t_n )∈Im(X)^N , ∃(x_n )∈X^N t_n =T(x_n ) (t_n ) etant convergente, c′est une suite de Cauchy. L′inegalite sur T permet de deduire (c′est chiant et trivial a ecrire donc je skip) que (x_n ) est aussi une suite de Cauchy. Or X est un espace de Banach, donc (x_n ) converge. Notant x_∞ cette limite Encore un coup d′inegalite chiante en utilisant l′inegalite de T, mais aussi la linearite de T et on obtient que T(x_∞ )=t_∞ d′ou on deduit la fermeture de Im(X)...
$$\left(\mathrm{2}\right)\Rightarrow\left(\mathrm{1}\right) \\ $$$$\mathrm{Soit}\:{c}\in\mathbb{R}^{\ast} \:\mathrm{tel}\:\mathrm{que}\:\forall{x}\in{X}\:\:\mid\mid{T}\left({x}\right)\mid\mid_{{Y}} \:\geqslant{c}\mid\mid{x}\mid\mid_{{X}} \\ $$$$\mathrm{Soit}\:\left({x},{x}'\right)\in{X}^{\mathrm{2}} \\ $$$$\mid\mid{T}\left({x}\right)−{T}\left({x}'\right)\mid\mid \\ $$$$=\mid\mid{T}\left({x}−{x}'\right)\mid\mid \\ $$$$\geqslant{c}\mid\mid{x}−{x}'\mid\mid \\ $$$$ \\ $$$${T}\left({x}\right)={T}\left({x}'\right) \\ $$$$\Rightarrow{T}\left({x}\right)−{T}\left({x}'\right)=\mathrm{0} \\ $$$$\Rightarrow\mid\mid{T}\left({x}\right)−{T}\left({x}'\right)\mid\mid=\mathrm{0} \\ $$$$\Rightarrow{c}\mid\mid{x}−{x}'\mid\mid=\mathrm{0} \\ $$$$\Rightarrow\mid\mid{x}−{x}'\mid\mid=\mathrm{0} \\ $$$$\Rightarrow{x}−{x}'=\mathrm{0} \\ $$$$\Rightarrow{x}={x}' \\ $$$$\mathrm{Donc}\:\left(\mathrm{2}\right)\Rightarrow\:{T}\:\:\mathrm{injectif} \\ $$$$ \\ $$$$\mathrm{Soit}\:\left({t}_{{n}} \right)\:\mathrm{une}\:\mathrm{suite}\:\mathrm{de}\:\mathrm{Im}\left({X}\right)\:\mathrm{convergente} \\ $$$$\mathrm{dans}\:{Y}. \\ $$$$\mathrm{Puisque}\:\left({t}_{{n}} \right)\in\mathrm{Im}\left({X}\right)^{\mathbb{N}} ,\:\:\exists\left({x}_{{n}} \right)\in{X}^{\mathbb{N}} \:{t}_{{n}} ={T}\left({x}_{{n}} \right) \\ $$$$\left({t}_{{n}} \right)\:\mathrm{etant}\:\mathrm{convergente},\:\mathrm{c}'\mathrm{est}\:\mathrm{une}\:\mathrm{suite}\:\mathrm{de}\: \\ $$$$\mathrm{Cauchy}. \\ $$$$\mathrm{L}'\mathrm{inegalite}\:\mathrm{sur}\:{T}\:\:\mathrm{permet}\:\mathrm{de}\:\mathrm{deduire}\: \\ $$$$\left(\mathrm{c}'\mathrm{est}\:\mathrm{chiant}\:\mathrm{et}\:\mathrm{trivial}\:\mathrm{a}\:\mathrm{ecrire}\:\mathrm{donc}\:\mathrm{je}\:\mathrm{skip}\right) \\ $$$$\mathrm{que}\:\left({x}_{{n}} \right)\:\mathrm{est}\:\mathrm{aussi}\:\mathrm{une}\:\mathrm{suite}\:\mathrm{de}\:\mathrm{Cauchy}. \\ $$$$\mathrm{Or}\:{X}\:\mathrm{est}\:\mathrm{un}\:\mathrm{espace}\:\mathrm{de}\:\mathrm{Banach},\:\mathrm{donc}\:\left({x}_{{n}} \right) \\ $$$$\mathrm{converge}.\:\mathrm{Notant}\:{x}_{\infty} \:\mathrm{cette}\:\mathrm{limite} \\ $$$$\mathrm{Encore}\:\mathrm{un}\:\mathrm{coup}\:\mathrm{d}'\mathrm{inegalite}\:\mathrm{chiante} \\ $$$$\mathrm{en}\:\mathrm{utilisant}\:\mathrm{l}'\mathrm{inegalite}\:\mathrm{de}\:{T},\:\mathrm{mais}\:\mathrm{aussi}\:\mathrm{la} \\ $$$$\mathrm{linearite}\:\mathrm{de}\:{T}\:\mathrm{et}\:\mathrm{on}\:\mathrm{obtient}\:\mathrm{que}\:{T}\left({x}_{\infty} \right)={t}_{\infty} \\ $$$$\mathrm{d}'\mathrm{ou}\:\mathrm{on}\:\mathrm{deduit}\:\mathrm{la}\:\mathrm{fermeture}\:\mathrm{de}\:\mathrm{Im}\left({X}\right)… \\ $$
Answered by TheHoneyCat last updated on 31/Mar/24
non(2) ⇒ non(1) Une facon de definir c est: c := Sup{Inf{c_x :∣∣T(x)∣∣≥c_x ∣∣x∣∣}, x∈X} Si (2) n′est pas verifie, on a tout simplement c=+∞. Donc on peut trouver (x_n ) tel que c_x_n →+∞ Donc (en renormalisant x_n et enlevant les termes nulles, pour avoir ∣∣T(x_n )∣∣=1) on obtient ∣∣T(x_n )∣∣ qui ne peut converger, car les x_n eux tendent vers 0. La encore j′explicite pas les inegalite par flemme. Mais je pense que c′est bon. si jamais vous redigez le detail et que ca marche pas... mettez moi en commentaire le souci et je mis met plus serieusement...
$$\mathrm{non}\left(\mathrm{2}\right)\:\Rightarrow\:\mathrm{non}\left(\mathrm{1}\right) \\ $$$$\mathrm{Une}\:\mathrm{facon}\:\mathrm{de}\:\mathrm{definir}\:{c}\:\mathrm{est}: \\ $$$${c}\::=\:\mathrm{Sup}\left\{\mathrm{Inf}\left\{{c}_{{x}} :\mid\mid{T}\left({x}\right)\mid\mid\geqslant{c}_{{x}} \mid\mid{x}\mid\mid\right\},\:{x}\in{X}\right\} \\ $$$$\mathrm{Si}\:\left(\mathrm{2}\right)\:\mathrm{n}'\mathrm{est}\:{pas}\:\mathrm{verifie},\:\mathrm{on}\:\mathrm{a}\:\mathrm{tout}\:\mathrm{simplement} \\ $$$${c}=+\infty. \\ $$$$ \\ $$$$\mathrm{Donc}\:\mathrm{on}\:\mathrm{peut}\:\mathrm{trouver}\:\left({x}_{{n}} \right)\:\mathrm{tel}\:\mathrm{que}\:{c}_{{x}_{{n}} } \rightarrow+\infty \\ $$$$\mathrm{Donc}\:\left(\mathrm{en}\:\mathrm{renormalisant}\:{x}_{{n}} \:\mathrm{et}\:\mathrm{enlevant}\:\mathrm{les}\right. \\ $$$$\left.\mathrm{termes}\:\mathrm{nulles},\:\mathrm{pour}\:\mathrm{avoir}\:\mid\mid{T}\left({x}_{{n}} \right)\mid\mid=\mathrm{1}\right)\:\mathrm{on}\:\mathrm{obtient} \\ $$$$\mid\mid{T}\left({x}_{{n}} \right)\mid\mid\:\mathrm{qui}\:\mathrm{ne}\:\mathrm{peut}\:\mathrm{converger},\:\mathrm{car}\:\mathrm{les}\:{x}_{{n}} \:\mathrm{eux} \\ $$$$\mathrm{tendent}\:\mathrm{vers}\:\mathrm{0}. \\ $$$$\mathrm{La}\:\mathrm{encore}\:\mathrm{j}'\mathrm{explicite}\:\mathrm{pas}\:\mathrm{les}\:\mathrm{inegalite}\:\mathrm{par}\:\mathrm{flemme}. \\ $$$$\mathrm{Mais}\:\mathrm{je}\:\mathrm{pense}\:\mathrm{que}\:\mathrm{c}'\mathrm{est}\:\mathrm{bon}. \\ $$$$ \\ $$$${si}\:{jamais}\:{vous}\:{redigez}\:\:{le}\:{detail}\:{et}\:{que}\:{ca} \\ $$$${marche}\:{pas}…\:{mettez}\:{moi}\:{en}\:{commentaire} \\ $$$${le}\:{souci}\:{et}\:{je}\:{mis}\:{met}\:{plus}\:{serieusement}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *