Question Number 205669 by hardmath last updated on 26/Mar/24
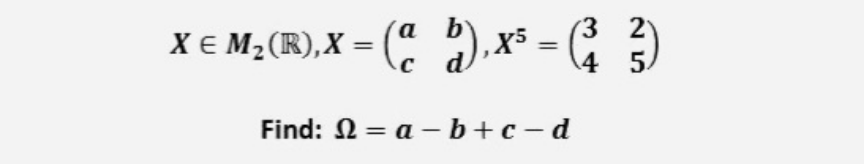
Answered by Berbere last updated on 27/Mar/24
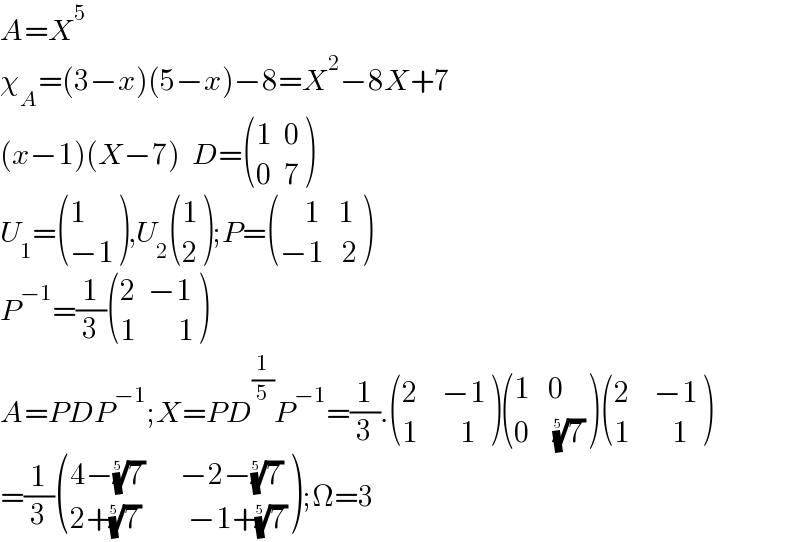
$${A}={X}^{\mathrm{5}} \\ $$$$\chi_{{A}} =\left(\mathrm{3}−{x}\right)\left(\mathrm{5}−{x}\right)−\mathrm{8}={X}^{\mathrm{2}} −\mathrm{8}{X}+\mathrm{7} \\ $$$$\left({x}−\mathrm{1}\right)\left({X}−\mathrm{7}\right)\:\:{D}=\begin{pmatrix}{\mathrm{1}\:\:\mathrm{0}}\\{\mathrm{0}\:\:\mathrm{7}}\end{pmatrix} \\ $$$${U}_{\mathrm{1}} =\begin{pmatrix}{\mathrm{1}}\\{−\mathrm{1}}\end{pmatrix},{U}_{\mathrm{2}} \begin{pmatrix}{\mathrm{1}}\\{\mathrm{2}}\end{pmatrix};{P}=\begin{pmatrix}{\:\:\:\:\mathrm{1}\:\:\:\mathrm{1}}\\{−\mathrm{1}\:\:\:\mathrm{2}}\end{pmatrix} \\ $$$${P}^{−\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{3}}\begin{pmatrix}{\mathrm{2}\:\:−\mathrm{1}}\\{\mathrm{1}\:\:\:\:\:\:\:\mathrm{1}}\end{pmatrix} \\ $$$${A}={PDP}^{−\mathrm{1}} ;{X}={PD}^{\frac{\mathrm{1}}{\mathrm{5}}} {P}^{−\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{3}}.\begin{pmatrix}{\mathrm{2}\:\:\:\:−\mathrm{1}}\\{\mathrm{1}\:\:\:\:\:\:\:\mathrm{1}}\end{pmatrix}\begin{pmatrix}{\mathrm{1}\:\:\:\mathrm{0}}\\{\mathrm{0}\:\:\:\:\sqrt[{\mathrm{5}}]{\mathrm{7}}}\end{pmatrix}\begin{pmatrix}{\mathrm{2}\:\:\:\:−\mathrm{1}}\\{\mathrm{1}\:\:\:\:\:\:\:\mathrm{1}}\end{pmatrix} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\begin{pmatrix}{\mathrm{4}−\sqrt[{\mathrm{5}}]{\mathrm{7}}\:\:\:\:\:\:−\mathrm{2}−\sqrt[{\mathrm{5}}]{\mathrm{7}}}\\{\mathrm{2}+\sqrt[{\mathrm{5}}]{\mathrm{7}}\:\:\:\:\:\:\:\:−\mathrm{1}+\sqrt[{\mathrm{5}}]{\mathrm{7}}}\end{pmatrix};\Omega=\mathrm{3} \\ $$
Commented by hardmath last updated on 27/Mar/24
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{dear}\:\mathrm{professor}\:\mathrm{cool} \\ $$
