Question Number 205670 by hardmath last updated on 26/Mar/24
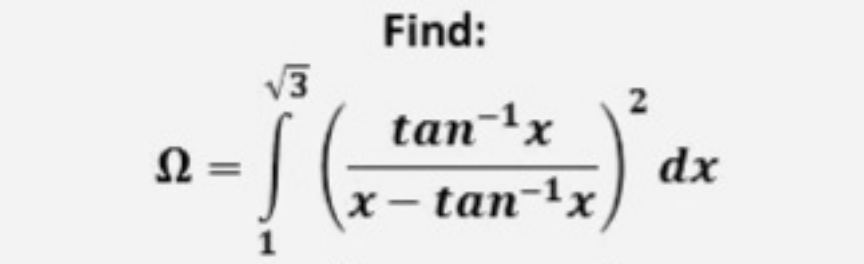
Answered by Berbere last updated on 27/Mar/24
![Ω=∫_1 ^(√3) (((tan^(−1) (x))/(x−tan^(−1) (x))))^2 dx ∫_1 ^(√3) (1+(x^2 /((x−tan^(−1) (x))^2 ))−((2x)/((x−tan^(−1) (x)))))dx =((√3)−1)+∫_1 ^(√3) ((−x^2 +2xtan^(−1) (x))/((x−tan^(−1) (x))^2 ))dx..E (1/((x−tan^(−1) (x))))=u;u′=((−(x^2 /(1+x^2 )))/((x−tan^(−1) (x))^2 )) E=((√3)−1)+∫_1 ^(√3) (((x^2 /((1+x^2 ))).(1+x^2 )−(1+x^2 )′.(−tan^(−1) (x)+x))/((x−tan^(−1) (x))^2 ))dx =((√3)−1)+∫_1 ^(√3) ( ((−(tan^(−1) (x)−x)′.(1+x^2 )+(1+x^2 )′(tan^(−1) (x)−x))/((x−tan^(−1) (x))))dx (√3)−1+[((x^2 +1)/(tan^(−1) (x)−x))]_1 ^(√3) =(√3)−1+((12)/(π−3(√3)))−(8/(π−4))](https://www.tinkutara.com/question/Q205678.png)
$$\Omega=\int_{\mathrm{1}} ^{\sqrt{\mathrm{3}}} \left(\frac{\mathrm{tan}^{−\mathrm{1}} \left({x}\right)}{{x}−\mathrm{tan}^{−\mathrm{1}} \left({x}\right)}\right)^{\mathrm{2}} {dx} \\ $$$$\int_{\mathrm{1}} ^{\sqrt{\mathrm{3}}} \left(\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\left({x}−\mathrm{tan}^{−\mathrm{1}} \left({x}\right)\right)^{\mathrm{2}} }−\frac{\mathrm{2}{x}}{\left({x}−\mathrm{tan}^{−\mathrm{1}} \left({x}\right)\right)}\right){dx} \\ $$$$=\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)+\int_{\mathrm{1}} ^{\sqrt{\mathrm{3}}} \frac{−{x}^{\mathrm{2}} +\mathrm{2}{x}\mathrm{tan}^{−\mathrm{1}} \left({x}\right)}{\left({x}−\mathrm{tan}^{−\mathrm{1}} \left({x}\right)\right)^{\mathrm{2}} }{dx}..{E} \\ $$$$\frac{\mathrm{1}}{\left({x}−\mathrm{tan}^{−\mathrm{1}} \left({x}\right)\right)}={u};{u}'=\frac{−\frac{{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} }}{\left({x}−\mathrm{tan}^{−\mathrm{1}} \left({x}\right)\right)^{\mathrm{2}} } \\ $$$${E}=\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)+\int_{\mathrm{1}} ^{\sqrt{\mathrm{3}}} \frac{\frac{{x}^{\mathrm{2}} }{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}.\left(\mathrm{1}+{x}^{\mathrm{2}} \right)−\left(\mathrm{1}+{x}^{\mathrm{2}} \right)'.\left(−\mathrm{tan}^{−\mathrm{1}} \left({x}\right)+{x}\right)}{\left({x}−\mathrm{tan}^{−\mathrm{1}} \left({x}\right)\right)^{\mathrm{2}} }{dx} \\ $$$$=\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)+\int_{\mathrm{1}} ^{\sqrt{\mathrm{3}}} \left(\:\frac{−\left(\mathrm{tan}^{−\mathrm{1}} \left({x}\right)−{x}\right)'.\left(\mathrm{1}+{x}^{\mathrm{2}} \right)+\left(\mathrm{1}+{x}^{\mathrm{2}} \right)'\left(\mathrm{tan}^{−\mathrm{1}} \left({x}\right)−{x}\right)}{\left({x}−\mathrm{tan}^{−\mathrm{1}} \left({x}\right)\right)}{dx}\right. \\ $$$$\sqrt{\mathrm{3}}−\mathrm{1}+\left[\frac{{x}^{\mathrm{2}} +\mathrm{1}}{\mathrm{tan}^{−\mathrm{1}} \left({x}\right)−{x}}\right]_{\mathrm{1}} ^{\sqrt{\mathrm{3}}} =\sqrt{\mathrm{3}}−\mathrm{1}+\frac{\mathrm{12}}{\pi−\mathrm{3}\sqrt{\mathrm{3}}}−\frac{\mathrm{8}}{\pi−\mathrm{4}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by hardmath last updated on 27/Mar/24
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{dear}\:\mathrm{professor}\:\mathrm{cool} \\ $$
