Question Number 205671 by hardmath last updated on 26/Mar/24

Answered by Berbere last updated on 27/Mar/24
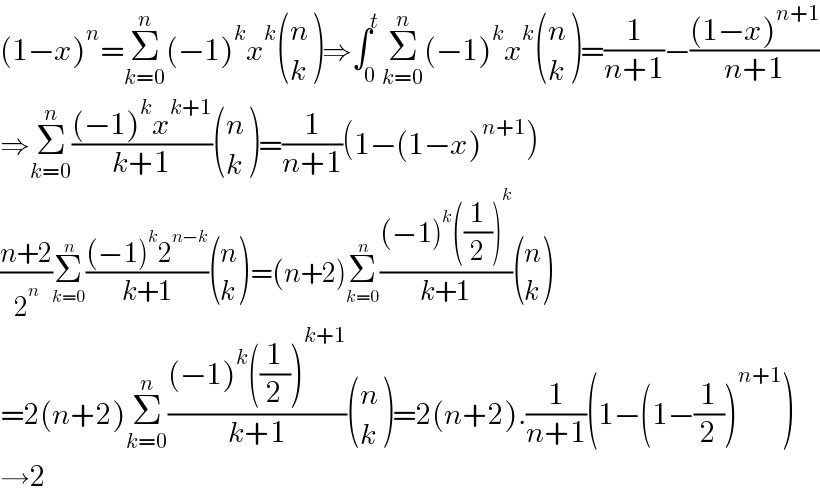
$$\left(\mathrm{1}−{x}\right)^{{n}} =\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\left(−\mathrm{1}\right)^{{k}} {x}^{{k}} \begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}\Rightarrow\int_{\mathrm{0}} ^{{t}} \underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\left(−\mathrm{1}\right)^{{k}} {x}^{{k}} \begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}=\frac{\mathrm{1}}{{n}+\mathrm{1}}−\frac{\left(\mathrm{1}−{x}\right)^{{n}+\mathrm{1}} }{{n}+\mathrm{1}} \\ $$$$\Rightarrow\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}} {x}^{{k}+\mathrm{1}} }{{k}+\mathrm{1}}\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}=\frac{\mathrm{1}}{{n}+\mathrm{1}}\left(\mathrm{1}−\left(\mathrm{1}−{x}\right)^{{n}+\mathrm{1}} \right) \\ $$$$\frac{{n}+\mathrm{2}}{\mathrm{2}^{{n}} }\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}} \mathrm{2}^{{n}−{k}} }{{k}+\mathrm{1}}\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}=\left({n}+\mathrm{2}\right)\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{k}} }{{k}+\mathrm{1}}\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix} \\ $$$$=\mathrm{2}\left({n}+\mathrm{2}\right)\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{k}+\mathrm{1}} }{{k}+\mathrm{1}}\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}=\mathrm{2}\left({n}+\mathrm{2}\right).\frac{\mathrm{1}}{{n}+\mathrm{1}}\left(\mathrm{1}−\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}+\mathrm{1}} \right) \\ $$$$\rightarrow\mathrm{2} \\ $$
Commented by hardmath last updated on 27/Mar/24
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{my}\:\mathrm{dear}\:\mathrm{professor}\:\mathrm{perfect} \\ $$
