Question Number 205672 by hardmath last updated on 26/Mar/24

Answered by Berbere last updated on 27/Mar/24
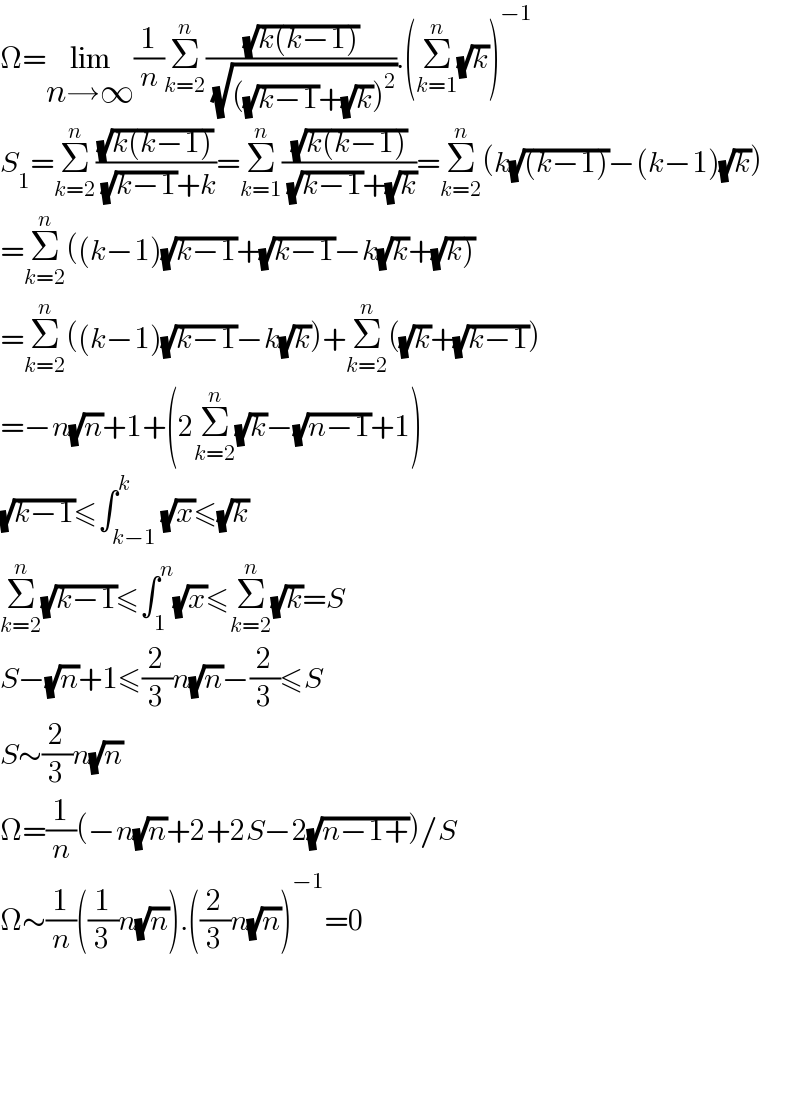
$$\Omega=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{n}}\underset{{k}=\mathrm{2}} {\overset{{n}} {\sum}}\frac{\sqrt{{k}\left({k}−\mathrm{1}\right)}}{\:\sqrt{\left(\sqrt{{k}−\mathrm{1}}+\sqrt{{k}}\right)^{\mathrm{2}} }}.\left(\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\sqrt{{k}}\right)^{−\mathrm{1}} \\ $$$${S}_{\mathrm{1}} =\underset{{k}=\mathrm{2}} {\overset{{n}} {\sum}}\frac{\sqrt{{k}\left({k}−\mathrm{1}\right)}}{\:\sqrt{{k}−\mathrm{1}}+{k}}=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\sqrt{{k}\left({k}−\mathrm{1}\right)}}{\:\sqrt{{k}−\mathrm{1}}+\sqrt{{k}}}=\underset{{k}=\mathrm{2}} {\overset{{n}} {\sum}}\left({k}\sqrt{\left({k}−\mathrm{1}\right)}−\left({k}−\mathrm{1}\right)\sqrt{{k}}\right) \\ $$$$=\underset{{k}=\mathrm{2}} {\overset{{n}} {\sum}}\left(\left({k}−\mathrm{1}\right)\sqrt{{k}−\mathrm{1}}+\sqrt{{k}−\mathrm{1}}−{k}\sqrt{{k}}+\sqrt{\left.{k}\right)}\right. \\ $$$$=\underset{{k}=\mathrm{2}} {\overset{{n}} {\sum}}\left(\left({k}−\mathrm{1}\right)\sqrt{{k}−\mathrm{1}}−{k}\sqrt{{k}}\right)+\underset{{k}=\mathrm{2}} {\overset{{n}} {\sum}}\left(\sqrt{{k}}+\sqrt{{k}−\mathrm{1}}\right) \\ $$$$=−{n}\sqrt{{n}}+\mathrm{1}+\left(\mathrm{2}\underset{{k}=\mathrm{2}} {\overset{{n}} {\sum}}\sqrt{{k}}−\sqrt{{n}−\mathrm{1}}+\mathrm{1}\right) \\ $$$$\sqrt{{k}−\mathrm{1}}\leqslant\int_{{k}−\mathrm{1}} ^{{k}} \sqrt{{x}}\leqslant\sqrt{{k}} \\ $$$$\underset{{k}=\mathrm{2}} {\overset{{n}} {\sum}}\sqrt{{k}−\mathrm{1}}\leqslant\int_{\mathrm{1}} ^{{n}} \sqrt{{x}}\leqslant\underset{{k}=\mathrm{2}} {\overset{{n}} {\sum}}\sqrt{{k}}={S} \\ $$$${S}−\sqrt{{n}}+\mathrm{1}\leqslant\frac{\mathrm{2}}{\mathrm{3}}{n}\sqrt{{n}}−\frac{\mathrm{2}}{\mathrm{3}}\leqslant{S} \\ $$$${S}\sim\frac{\mathrm{2}}{\mathrm{3}}{n}\sqrt{{n}} \\ $$$$\Omega=\frac{\mathrm{1}}{{n}}\left(−{n}\sqrt{{n}}+\mathrm{2}+\mathrm{2}{S}−\mathrm{2}\sqrt{{n}−\mathrm{1}+}\right)/{S} \\ $$$$\Omega\sim\frac{\mathrm{1}}{{n}}\left(\frac{\mathrm{1}}{\mathrm{3}}{n}\sqrt{{n}}\right).\left(\frac{\mathrm{2}}{\mathrm{3}}{n}\sqrt{{n}}\right)^{−\mathrm{1}} =\mathrm{0} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by hardmath last updated on 27/Mar/24
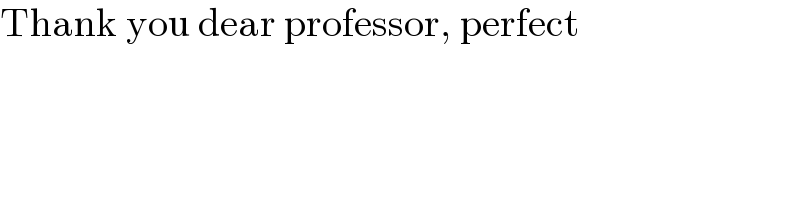
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{dear}\:\mathrm{professor},\:\mathrm{perfect} \\ $$
Commented by Berbere last updated on 27/Mar/24

$${Withe}\:{Pleasur} \\ $$
