Question Number 205681 by naka3546 last updated on 27/Mar/24
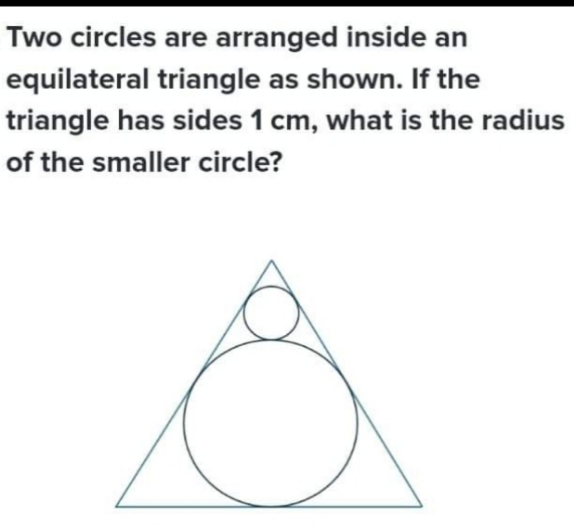
Answered by mr W last updated on 27/Mar/24
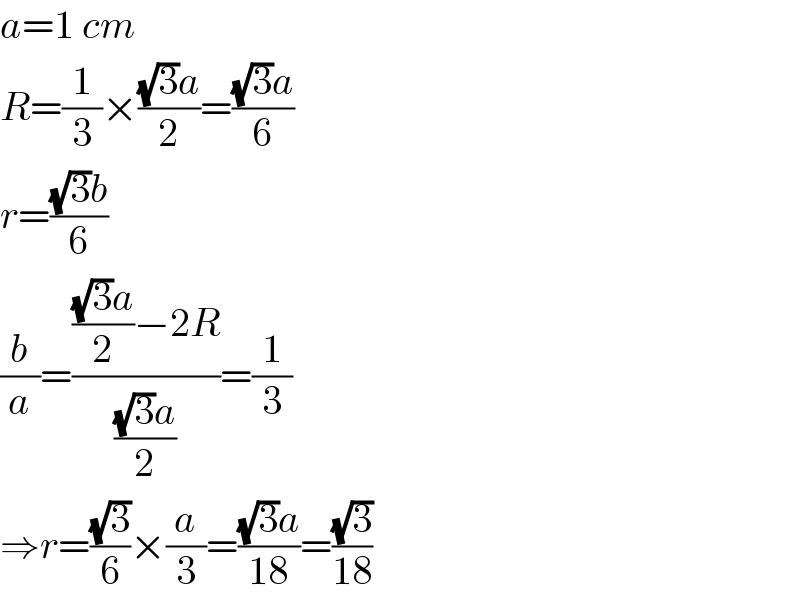
$${a}=\mathrm{1}\:{cm} \\ $$$${R}=\frac{\mathrm{1}}{\mathrm{3}}×\frac{\sqrt{\mathrm{3}}{a}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}{a}}{\mathrm{6}} \\ $$$${r}=\frac{\sqrt{\mathrm{3}}{b}}{\mathrm{6}} \\ $$$$\frac{{b}}{{a}}=\frac{\frac{\sqrt{\mathrm{3}}{a}}{\mathrm{2}}−\mathrm{2}{R}}{\frac{\sqrt{\mathrm{3}}{a}}{\mathrm{2}}}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\Rightarrow{r}=\frac{\sqrt{\mathrm{3}}}{\mathrm{6}}×\frac{{a}}{\mathrm{3}}=\frac{\sqrt{\mathrm{3}}{a}}{\mathrm{18}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{18}} \\ $$
Commented by naka3546 last updated on 27/Mar/24

$$\mathrm{Thank}\:\mathrm{you},\:\mathrm{sir}. \\ $$
Answered by A5T last updated on 27/Mar/24

Commented by A5T last updated on 27/Mar/24
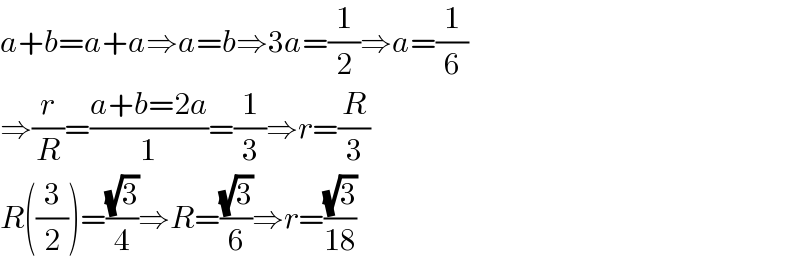
$${a}+{b}={a}+{a}\Rightarrow{a}={b}\Rightarrow\mathrm{3}{a}=\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow{a}=\frac{\mathrm{1}}{\mathrm{6}} \\ $$$$\Rightarrow\frac{{r}}{{R}}=\frac{{a}+{b}=\mathrm{2}{a}}{\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{3}}\Rightarrow{r}=\frac{{R}}{\mathrm{3}} \\ $$$${R}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)=\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\Rightarrow{R}=\frac{\sqrt{\mathrm{3}}}{\mathrm{6}}\Rightarrow{r}=\frac{\sqrt{\mathrm{3}}}{\mathrm{18}} \\ $$
