Menu Close

lim-n-2n-1-2n-3-4n-1-2n-2n-2-4n-

Tinku Tara 0 Comments
Pin




Question Number 205716 by universe last updated on 28/Mar/24
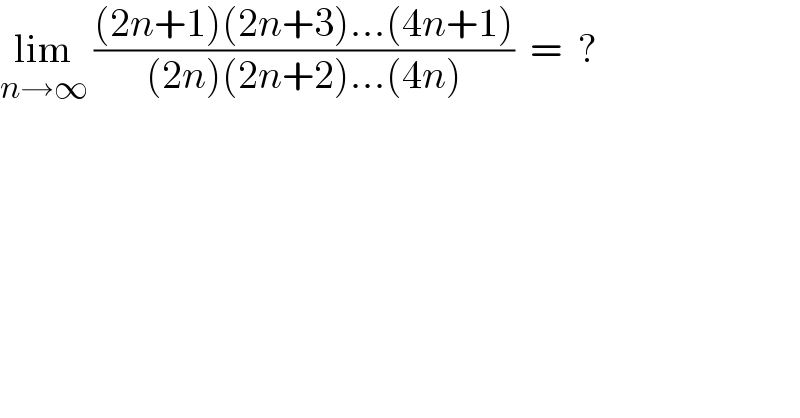
lim_(n→∞) (((2n+1)(2n+3)...(4n+1))/((2n)(2n+2)...(4n))) = ?
$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{\left(\mathrm{2}{n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{3}\right)…\left(\mathrm{4}{n}+\mathrm{1}\right)}{\left(\mathrm{2}{n}\right)\left(\mathrm{2}{n}+\mathrm{2}\right)…\left(\mathrm{4}{n}\right)}\:\:=\:\:? \\ $$
Answered by MM42 last updated on 28/Mar/24
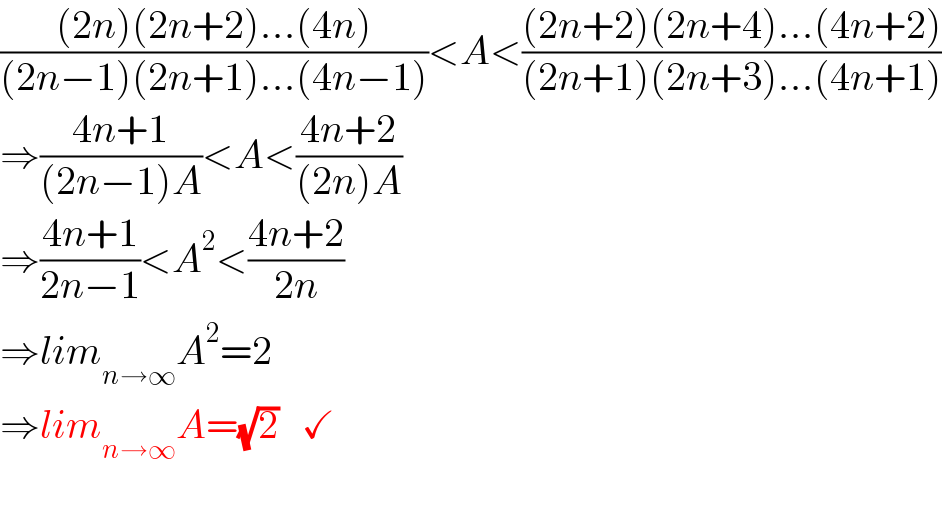
(((2n)(2n+2)...(4n))/((2n−1)(2n+1)...(4n−1)))<A<(((2n+2)(2n+4)...(4n+2))/((2n+1)(2n+3)...(4n+1))) ⇒((4n+1)/((2n−1)A))<A<((4n+2)/((2n)A)) ⇒((4n+1)/(2n−1))<A^2 <((4n+2)/(2n)) ⇒lim_(n→∞) A^2 =2 ⇒lim_(n→∞) A=(√2) ✓
$$\frac{\left(\mathrm{2}{n}\right)\left(\mathrm{2}{n}+\mathrm{2}\right)…\left(\mathrm{4}{n}\right)}{\left(\mathrm{2}{n}−\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)…\left(\mathrm{4}{n}−\mathrm{1}\right)}<{A}<\frac{\left(\mathrm{2}{n}+\mathrm{2}\right)\left(\mathrm{2}{n}+\mathrm{4}\right)…\left(\mathrm{4}{n}+\mathrm{2}\right)}{\left(\mathrm{2}{n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{3}\right)…\left(\mathrm{4}{n}+\mathrm{1}\right)} \\ $$$$\Rightarrow\frac{\mathrm{4}{n}+\mathrm{1}}{\left(\mathrm{2}{n}−\mathrm{1}\right){A}}<{A}<\frac{\mathrm{4}{n}+\mathrm{2}}{\left(\mathrm{2}{n}\right){A}} \\ $$$$\Rightarrow\frac{\mathrm{4}{n}+\mathrm{1}}{\mathrm{2}{n}−\mathrm{1}}<{A}^{\mathrm{2}} <\frac{\mathrm{4}{n}+\mathrm{2}}{\mathrm{2}{n}} \\ $$$$\Rightarrow{lim}_{{n}\rightarrow\infty} {A}^{\mathrm{2}} =\mathrm{2} \\ $$$$\Rightarrow{lim}_{{n}\rightarrow\infty} {A}=\sqrt{\mathrm{2}}\:\:\:\checkmark\: \\ $$$$ \\ $$
Answered by Berbere last updated on 28/Mar/24
=lim_(n→∞) Π_(k=0) ^n (((2n+2k+1))/((2n+2k)))=lim_(n→∞) U_n U_n =e^(Σ_(k=0) ^n ln(((2k+2n+1)/(2n+2k)))) =e^(Σ_(k=0) ^n ln(1+(1/(2n+2k)))) =e^V_n ∀x∈[0,1[ x−(x^2 /2)≤ln(1+x)≤x; proof (1−x^2 )≤1 ⇒1−x≤(1/(1+x))⇒∫_0 ^t 1−x≤∫_0 ^t (dx/(1+x)) ⇔t−(t^2 /2)≤ln(1+x);(1/(1+x))≤1⇒ln(1+x)≤x ⇒ (1/(2(n+k)))−(1/(8(n+k)^2 ))≤ln(1+(1/(2(n+k))))≤(1/(2(n+k))) ⇒ (1/(2n))Σ_(k=0) ^n (1/(1+(k/n)))−(1/8)T_n ≤ V_n ≤(1/(2n))Σ_(k=0) ^n (1/(1+(k/n))) 0≤T_n =Σ_(k=0) ^n (1/((n+k)^2 ))≤((n+1)/n^2 )→0 lim_(n→∞) V_n =lim_(n→∞) (1/(2n))Σ_(k=0) ^n (1/(1+(k/n)))Riemann Sum=(1/2)∫_0 ^1 (1/(1+x))dx=((ln(2))/2) U_n =lim_(n→∞) e^V_n =e^((1/2)ln(2)) =(√2)
$$=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\underset{{k}=\mathrm{0}} {\overset{{n}} {\prod}}\frac{\left(\mathrm{2}{n}+\mathrm{2}{k}+\mathrm{1}\right)}{\left(\mathrm{2}{n}+\mathrm{2}{k}\right)}=\underset{{n}\rightarrow\infty} {\mathrm{lim}}{U}_{{n}} \\ $$$${U}_{{n}} ={e}^{\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{ln}\left(\frac{\mathrm{2}{k}+\mathrm{2}{n}+\mathrm{1}}{\mathrm{2}{n}+\mathrm{2}{k}}\right)} ={e}^{\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{2}{k}}\right)} ={e}^{{V}_{{n}} } \\ $$$$\forall{x}\in\left[\mathrm{0},\mathrm{1}\left[\right.\right. \\ $$$${x}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\leqslant{ln}\left(\mathrm{1}+{x}\right)\leqslant{x}; \\ $$$${proof}\:\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\leqslant\mathrm{1}\:\Rightarrow\mathrm{1}−{x}\leqslant\frac{\mathrm{1}}{\mathrm{1}+{x}}\Rightarrow\int_{\mathrm{0}} ^{{t}} \mathrm{1}−{x}\leqslant\int_{\mathrm{0}} ^{{t}} \frac{{dx}}{\mathrm{1}+{x}} \\ $$$$\Leftrightarrow{t}−\frac{{t}^{\mathrm{2}} }{\mathrm{2}}\leqslant{ln}\left(\mathrm{1}+{x}\right);\frac{\mathrm{1}}{\mathrm{1}+{x}}\leqslant\mathrm{1}\Rightarrow{ln}\left(\mathrm{1}+{x}\right)\leqslant{x} \\ $$$$\Rightarrow\:\:\frac{\mathrm{1}}{\mathrm{2}\left({n}+{k}\right)}−\frac{\mathrm{1}}{\mathrm{8}\left({n}+{k}\right)^{\mathrm{2}} }\leqslant{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}\left({n}+{k}\right)}\right)\leqslant\frac{\mathrm{1}}{\mathrm{2}\left({n}+{k}\right)} \\ $$$$\Rightarrow\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}{n}}\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{1}+\frac{{k}}{{n}}}−\frac{\mathrm{1}}{\mathrm{8}}{T}_{{n}} \leqslant\:{V}_{{n}} \leqslant\frac{\mathrm{1}}{\mathrm{2}{n}}\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{1}+\frac{{k}}{{n}}} \\ $$$$\mathrm{0}\leqslant{T}_{{n}} =\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\left({n}+{k}\right)^{\mathrm{2}} }\leqslant\frac{{n}+\mathrm{1}}{{n}^{\mathrm{2}} }\rightarrow\mathrm{0} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}{V}_{{n}} =\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{2}{n}}\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{1}+\frac{{k}}{{n}}}{Riemann}\:{Sum}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+{x}}{dx}=\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{2}} \\ $$$${U}_{{n}} =\underset{{n}\rightarrow\infty} {\mathrm{lim}}{e}^{{V}_{{n}} } ={e}^{\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{2}\right)} =\sqrt{\mathrm{2}} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *