Question Number 206216 by cortano21 last updated on 09/Apr/24
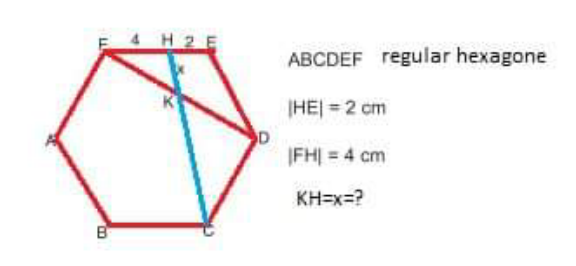
Answered by A5T last updated on 09/Apr/24

$${HC}=\sqrt{\mathrm{108}+\mathrm{4}}=\sqrt{\mathrm{112}}=\mathrm{4}\sqrt{\mathrm{7}} \\ $$$${Let}\:{HC}\:{meet}\:{the}\:{circumcircle}\:{of}\:{the}\:{hexagon} \\ $$$${at}\:{L}\:{then},\:{HC}×{HL}={FH}×{HE}=\mathrm{8}\Rightarrow{HL}=\frac{\mathrm{2}\sqrt{\mathrm{7}}}{\mathrm{7}} \\ $$$${sin}\angle{EHC}=\frac{\sqrt{\mathrm{108}}}{\:\sqrt{\mathrm{112}}}=\frac{\mathrm{3}\sqrt{\mathrm{21}}}{\mathrm{14}}\Rightarrow{cos}\angle{EHC}=\frac{\sqrt{\mathrm{7}}}{\mathrm{14}} \\ $$$$\Rightarrow\sqrt{{x}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} −\mathrm{4}{x}\frac{\sqrt{\mathrm{7}}}{\mathrm{14}}}=\sqrt{{KD}^{\mathrm{2}} +\mathrm{6}^{\mathrm{2}} −\mathrm{6}\sqrt{\mathrm{3}}×{KD}} \\ $$$$\Rightarrow{x}^{\mathrm{2}} +\mathrm{4}−\frac{\mathrm{2}{x}\sqrt{\mathrm{7}}}{\mathrm{7}}={KD}^{\mathrm{2}} +\mathrm{36}−\mathrm{6}\sqrt{\mathrm{3}}{KD}…\left({i}\right) \\ $$$${FK}×{KD}={KC}×{KL} \\ $$$$\Rightarrow\left(\sqrt{\mathrm{108}}−{KD}\right){KD}=\left(\mathrm{4}\sqrt{\mathrm{7}}−{x}\right)\left({x}+\frac{\mathrm{2}\sqrt{\mathrm{7}}}{\mathrm{7}}\right) \\ $$$$\Rightarrow\mathrm{6}\sqrt{\mathrm{3}}{KD}−{KD}^{\mathrm{2}} =\mathrm{4}{x}\sqrt{\mathrm{7}}+\mathrm{8}−{x}^{\mathrm{2}} −\frac{\mathrm{2}{x}\sqrt{\mathrm{7}}}{\mathrm{7}}…\left({ii}\right) \\ $$$$\left({i}\right)\&\left({ii}\right)\Rightarrow\mathrm{32}+\frac{\mathrm{2}{x}\sqrt{\mathrm{7}}}{\:\mathrm{7}}=\mathrm{4}{x}\sqrt{\mathrm{7}}+\mathrm{8}−\frac{\mathrm{2}{x}\sqrt{\mathrm{7}}}{\mathrm{7}} \\ $$$$\Rightarrow{x}=\sqrt{\mathrm{7}}\approx\mathrm{2}.\mathrm{64575} \\ $$
Answered by mr W last updated on 09/Apr/24

Commented by mr W last updated on 09/Apr/24

$${HC}=\sqrt{\mathrm{12}^{\mathrm{2}} +\mathrm{8}^{\mathrm{2}} −\mathrm{12}×\mathrm{8}}=\mathrm{4}\sqrt{\mathrm{7}} \\ $$$$\frac{{x}}{{y}}×\frac{\mathrm{6}}{\mathrm{6}}×\frac{\mathrm{12}}{\mathrm{4}}=\mathrm{1} \\ $$$$\Rightarrow\frac{{x}}{{y}}=\frac{\mathrm{1}}{\mathrm{3}}\:\Rightarrow\frac{{x}}{{x}+{y}}=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\Rightarrow{x}=\frac{{HC}}{\mathrm{4}}=\sqrt{\mathrm{7}} \\ $$
Answered by cortano21 last updated on 10/Apr/24

Commented by mr W last updated on 10/Apr/24

$${FK}=\frac{{FD}}{\mathrm{2}}\:{is}\:{not}\:{obvious},\:{must}\:{be} \\ $$$${proved}\:{at}\:{first}. \\ $$
Commented by A5T last updated on 10/Apr/24

$$\frac{\mathrm{4}}{\mathrm{8}}×\frac{\mathrm{12}}{\mathrm{6}}×\frac{{DK}}{{KF}}=\mathrm{1}\Rightarrow{DK}={KF}\Rightarrow{FK}=\frac{{FD}}{\mathrm{2}} \\ $$
