Question-206232

Question Number 206232 by mr W last updated on 09/Apr/24

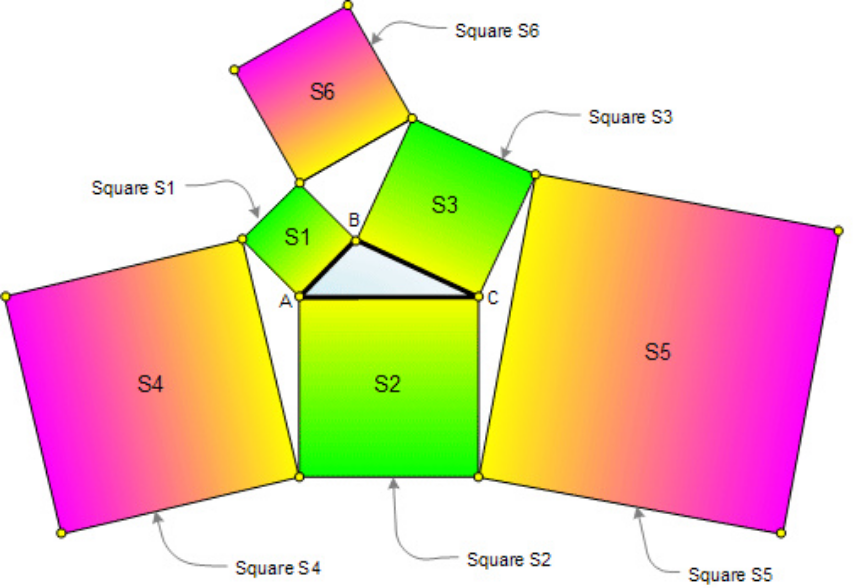
Answered by A5T last updated on 09/Apr/24

S_2 =S_1 +S_3 −2AB×BCcos(θ) S_1 =S_2 +S_3 −2BC×ACcos(β) S_3 =S_2 +S_1 +2AB×ACcos(θ+β) S_4 =S_1 +S_2 −2AB×ACcos(θ+β) S_5 =S_3 +S_2 +2AC×BCcosβ S_6 =S_1 +S_3 +2AB×BCcosθ ⇒S_1 +S_2 +...+S_6 =4(S_1 +S_2 +S_3 ) ⇒S_4 +S_5 +S_6 =3(S_1 +S_2 +S_3 )=30

$${S}_{\mathrm{2}} ={S}_{\mathrm{1}} +{S}_{\mathrm{3}} −\mathrm{2}{AB}×{BCcos}\left(\theta\right) \\ $$$${S}_{\mathrm{1}} ={S}_{\mathrm{2}} +{S}_{\mathrm{3}} −\mathrm{2}{BC}×{ACcos}\left(\beta\right) \\ $$$${S}_{\mathrm{3}} ={S}_{\mathrm{2}} +{S}_{\mathrm{1}} +\mathrm{2}{AB}×{ACcos}\left(\theta+\beta\right) \\ $$$${S}_{\mathrm{4}} ={S}_{\mathrm{1}} +{S}_{\mathrm{2}} −\mathrm{2}{AB}×{ACcos}\left(\theta+\beta\right) \\ $$$${S}_{\mathrm{5}} ={S}_{\mathrm{3}} +{S}_{\mathrm{2}} +\mathrm{2}{AC}×{BCcos}\beta \\ $$$${S}_{\mathrm{6}} ={S}_{\mathrm{1}} +{S}_{\mathrm{3}} +\mathrm{2}{AB}×{BCcos}\theta \\ $$$$\Rightarrow{S}_{\mathrm{1}} +{S}_{\mathrm{2}} +…+{S}_{\mathrm{6}} =\mathrm{4}\left({S}_{\mathrm{1}} +{S}_{\mathrm{2}} +{S}_{\mathrm{3}} \right) \\ $$$$\Rightarrow{S}_{\mathrm{4}} +{S}_{\mathrm{5}} +{S}_{\mathrm{6}} =\mathrm{3}\left({S}_{\mathrm{1}} +{S}_{\mathrm{2}} +{S}_{\mathrm{3}} \right)=\mathrm{30} \\ $$

Commented by mr W last updated on 09/Apr/24

$${great}! \\ $$

Answered by mr W last updated on 09/Apr/24

if S_1 +S_2 +S_3 =10, find S_4 +S_5 +S_6 =?

$${if}\:{S}_{\mathrm{1}} +{S}_{\mathrm{2}} +{S}_{\mathrm{3}} =\mathrm{10},\:{find}\:{S}_{\mathrm{4}} +{S}_{\mathrm{5}} +{S}_{\mathrm{6}} =? \\ $$

Answered by mr W last updated on 10/Apr/24

Commented by mr W last updated on 10/Apr/24

f^2 =a^2 +b^2 −2ab cos (180°−γ)=a^2 +b^2 +2ab cos γ c^2 =a^2 +b^2 −2ab cos γ f^2 +c^2 =2(a^2 +b^2 ) similarly e^2 +b^2 =2(c^2 +a^2 ) d^2 +a^2 =2(b^2 +c^2 ) ⇒d^2 +e^2 +f^2 +a^2 +b^2 +c^2 =4(a^2 +b^2 +c^2 ) ⇒d^2 +e^2 +f^2 =3(a^2 +b^2 +c^2 ) ⇒S_4 +S_5 +S_6 =3(S_1 +S_2 +S_3 )=30

$${f}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}\:\mathrm{cos}\:\left(\mathrm{180}°−\gamma\right)={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}{ab}\:\mathrm{cos}\:\gamma \\ $$$${c}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}\:\mathrm{cos}\:\gamma \\ $$$${f}^{\mathrm{2}} +{c}^{\mathrm{2}} =\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right) \\ $$$${similarly} \\ $$$${e}^{\mathrm{2}} +{b}^{\mathrm{2}} =\mathrm{2}\left({c}^{\mathrm{2}} +{a}^{\mathrm{2}} \right) \\ $$$${d}^{\mathrm{2}} +{a}^{\mathrm{2}} =\mathrm{2}\left({b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right) \\ $$$$\Rightarrow{d}^{\mathrm{2}} +{e}^{\mathrm{2}} +{f}^{\mathrm{2}} +{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} =\mathrm{4}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right) \\ $$$$\Rightarrow{d}^{\mathrm{2}} +{e}^{\mathrm{2}} +{f}^{\mathrm{2}} =\mathrm{3}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right) \\ $$$$\Rightarrow{S}_{\mathrm{4}} +{S}_{\mathrm{5}} +{S}_{\mathrm{6}} =\mathrm{3}\left({S}_{\mathrm{1}} +{S}_{\mathrm{2}} +{S}_{\mathrm{3}} \right)=\mathrm{30} \\ $$

Answered by TonyCWX08 last updated on 11/Apr/24

((S_4 +S_5 +S_6 )/(S_1 +S_2 +S_3 ))=3 ((S_4 +S_5 +S_6 )/(10))=3 S_4 +S_5 +S_6 =30

$$\frac{{S}_{\mathrm{4}} +{S}_{\mathrm{5}} +{S}_{\mathrm{6}} }{{S}_{\mathrm{1}} +{S}_{\mathrm{2}} +{S}_{\mathrm{3}} }=\mathrm{3} \\ $$$$\frac{{S}_{\mathrm{4}} +{S}_{\mathrm{5}} +{S}_{\mathrm{6}} }{\mathrm{10}}=\mathrm{3} \\ $$$${S}_{\mathrm{4}} +{S}_{\mathrm{5}} +{S}_{\mathrm{6}} =\mathrm{30} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply