Question-206292

Question Number 206292 by cortano21 last updated on 11/Apr/24

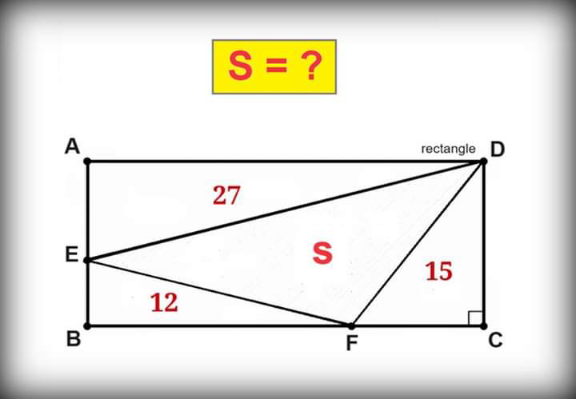
Answered by A5T last updated on 11/Apr/24

Let AE=x;BE=y;BF=v;FC=w S+39=(((2v+w)(x+y))/2)=((2v(x+y))/2)+15⇒S=vx wx=54−S=30−yw⇒yw=S−24 (([BFD])/([DFC]))=(v/w)⇒[BFD]=((15v)/w) (([EDB])/([ADE[))=(y/x)⇒EDB=((27y)/x) ⇒((15v)/w)+((27y)/x)=S+12⇒((15S+27(S−24))/(54−S))=S+12 ⇒S=36

$${Let}\:{AE}={x};{BE}={y};{BF}={v};{FC}={w} \\ $$$${S}+\mathrm{39}=\frac{\left(\mathrm{2}{v}+{w}\right)\left({x}+{y}\right)}{\mathrm{2}}=\frac{\mathrm{2}{v}\left({x}+{y}\right)}{\mathrm{2}}+\mathrm{15}\Rightarrow{S}={vx} \\ $$$${wx}=\mathrm{54}−{S}=\mathrm{30}−{yw}\Rightarrow{yw}={S}−\mathrm{24} \\ $$$$\frac{\left[{BFD}\right]}{\left[{DFC}\right]}=\frac{{v}}{{w}}\Rightarrow\left[{BFD}\right]=\frac{\mathrm{15}{v}}{{w}} \\ $$$$\frac{\left[{EDB}\right]}{\left[{ADE}\left[\right.\right.}=\frac{{y}}{{x}}\Rightarrow{EDB}=\frac{\mathrm{27}{y}}{{x}} \\ $$$$\Rightarrow\frac{\mathrm{15}{v}}{{w}}+\frac{\mathrm{27}{y}}{{x}}={S}+\mathrm{12}\Rightarrow\frac{\mathrm{15}{S}+\mathrm{27}\left({S}−\mathrm{24}\right)}{\mathrm{54}−{S}}={S}+\mathrm{12} \\ $$$$\Rightarrow{S}=\mathrm{36} \\ $$

Answered by mr W last updated on 11/Apr/24

Commented by mr W last updated on 11/Apr/24

(a+b)c=2A ⇒ac=2A−bc b(c+d)=2C ⇒bd=2C−bc ad=2B abcd=(2A−bc)(2C−bc) 2B(bc)=4AC−2(A+C)(bc)+(bc)^2 4AC−2(A+B+C)(bc)+(bc)^2 =0 ⇒bc=(A+B+C)−(√((A+B+C)^2 −4AC)) S=(a+b)(c+d)−(A+B+C) S=((4AC)/(bc))−(A+B+C) S=((4AC)/((A+B+C)−(√((A+B+C)^2 −4AC))))−(A+B+C) S=(A+B+C)+(√((A+B+C)^2 −4AC))−(A+B+C) ⇒S=(√((A+B+C)^2 −4AC)) =(√((27+12+25)^2 −4×27×15))=36

$$\left({a}+{b}\right){c}=\mathrm{2}{A}\:\Rightarrow{ac}=\mathrm{2}{A}−{bc} \\ $$$${b}\left({c}+{d}\right)=\mathrm{2}{C}\:\Rightarrow{bd}=\mathrm{2}{C}−{bc} \\ $$$${ad}=\mathrm{2}{B} \\ $$$${abcd}=\left(\mathrm{2}{A}−{bc}\right)\left(\mathrm{2}{C}−{bc}\right) \\ $$$$\mathrm{2}{B}\left({bc}\right)=\mathrm{4}{AC}−\mathrm{2}\left({A}+{C}\right)\left({bc}\right)+\left({bc}\right)^{\mathrm{2}} \\ $$$$\mathrm{4}{AC}−\mathrm{2}\left({A}+{B}+{C}\right)\left({bc}\right)+\left({bc}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{bc}=\left({A}+{B}+{C}\right)−\sqrt{\left({A}+{B}+{C}\right)^{\mathrm{2}} −\mathrm{4}{AC}} \\ $$$$ \\ $$$${S}=\left({a}+{b}\right)\left({c}+{d}\right)−\left({A}+{B}+{C}\right) \\ $$$${S}=\frac{\mathrm{4}{AC}}{{bc}}−\left({A}+{B}+{C}\right) \\ $$$${S}=\frac{\mathrm{4}{AC}}{\left({A}+{B}+{C}\right)−\sqrt{\left({A}+{B}+{C}\right)^{\mathrm{2}} −\mathrm{4}{AC}}}−\left({A}+{B}+{C}\right) \\ $$$${S}=\left({A}+{B}+{C}\right)+\sqrt{\left({A}+{B}+{C}\right)^{\mathrm{2}} −\mathrm{4}{AC}}−\left({A}+{B}+{C}\right) \\ $$$$\Rightarrow{S}=\sqrt{\left({A}+{B}+{C}\right)^{\mathrm{2}} −\mathrm{4}{AC}} \\ $$$$\:\:\:\:\:\:\:\:=\sqrt{\left(\mathrm{27}+\mathrm{12}+\mathrm{25}\right)^{\mathrm{2}} −\mathrm{4}×\mathrm{27}×\mathrm{15}}=\mathrm{36} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply