Question Number 206396 by cortano21 last updated on 13/Apr/24
Answered by mr W last updated on 13/Apr/24

Commented by mr W last updated on 13/Apr/24

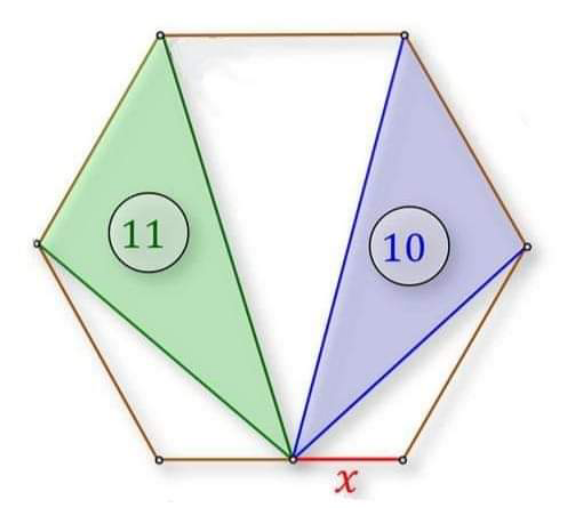
$${a}={side}\:{length}\:{of}\:{hexagon} \\ $$$${C}=\mathrm{2}×\frac{\sqrt{\mathrm{3}}{a}^{\mathrm{2}} }{\mathrm{4}} \\ $$$${A}+{B}=\frac{\sqrt{\mathrm{3}}{a}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\mathrm{11}+\mathrm{10}=\mathrm{6}×\frac{\sqrt{\mathrm{3}}{a}^{\mathrm{2}} }{\mathrm{4}}−{A}−{B}−{C}=\mathrm{3}×\frac{\sqrt{\mathrm{3}}{a}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\Rightarrow\sqrt{\mathrm{3}}{a}^{\mathrm{2}} =\mathrm{28}\:\Rightarrow{a}=\sqrt{\frac{\mathrm{28}}{\:\sqrt{\mathrm{3}}}} \\ $$$$\frac{{A}+\mathrm{11}−\frac{\sqrt{\mathrm{3}}{a}^{\mathrm{2}} }{\mathrm{4}}}{{B}+\mathrm{10}−\frac{\sqrt{\mathrm{3}}{a}^{\mathrm{2}} }{\mathrm{4}}}=\frac{{a}−{x}}{{x}}=\frac{{A}}{{B}} \\ $$$$\frac{{A}+\mathrm{11}−\mathrm{7}}{{B}+\mathrm{10}−\mathrm{7}}=\frac{{A}}{{B}} \\ $$$$\Rightarrow\frac{{A}}{{B}}=\frac{\mathrm{4}}{\mathrm{3}}=\frac{{a}−{x}}{{x}} \\ $$$$\Rightarrow\frac{{x}}{{a}}=\frac{\mathrm{3}}{\mathrm{7}} \\ $$$$\Rightarrow{x}=\frac{\mathrm{3}}{\mathrm{7}}×\sqrt{\frac{\mathrm{28}}{\:\sqrt{\mathrm{3}}}}=\frac{\mathrm{2}\sqrt{\mathrm{21}\sqrt{\mathrm{3}}}}{\:\mathrm{7}}\approx\mathrm{1}.\mathrm{723}\:\checkmark \\ $$
Commented by cortano21 last updated on 13/Apr/24

$$\:\gtrdot\cancel{\underline{ }} \\ $$
Commented by mr W last updated on 13/Apr/24
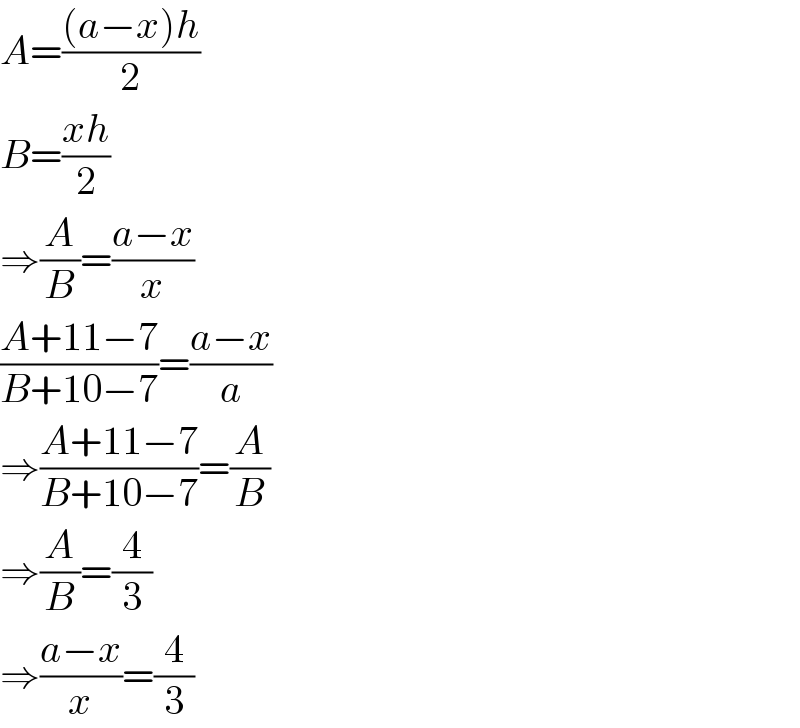
$${A}=\frac{\left({a}−{x}\right){h}}{\mathrm{2}} \\ $$$${B}=\frac{{xh}}{\mathrm{2}} \\ $$$$\Rightarrow\frac{{A}}{{B}}=\frac{{a}−{x}}{{x}} \\ $$$$\frac{{A}+\mathrm{11}−\mathrm{7}}{{B}+\mathrm{10}−\mathrm{7}}=\frac{{a}−{x}}{{a}} \\ $$$$\Rightarrow\frac{{A}+\mathrm{11}−\mathrm{7}}{{B}+\mathrm{10}−\mathrm{7}}=\frac{{A}}{{B}} \\ $$$$\Rightarrow\frac{{A}}{{B}}=\frac{\mathrm{4}}{\mathrm{3}} \\ $$$$\Rightarrow\frac{{a}−{x}}{{x}}=\frac{\mathrm{4}}{\mathrm{3}} \\ $$
Commented by cortano21 last updated on 13/Apr/24

$$\:\:\cancel{\underline{\underbrace{\boldsymbol{\mathfrak{f}}}}} \\ $$
Commented by mr W last updated on 13/Apr/24

$$\frac{{A}+\mathrm{4}}{{B}+\mathrm{3}}=\frac{{A}}{{B}} \\ $$$$\Rightarrow{AB}+\mathrm{4}{B}={AB}+\mathrm{3}{A} \\ $$$$\Rightarrow\mathrm{4}{B}=\mathrm{3}{A} \\ $$$$\Rightarrow\frac{{A}}{{B}}=\frac{\mathrm{4}}{\mathrm{3}} \\ $$
Commented by cortano21 last updated on 13/Apr/24

$$\:\:\underline{\underbrace{ }} \\ $$
Commented by cortano21 last updated on 17/Apr/24

$$\:\:\Rightarrow\:\frac{\mathrm{11}}{\mathrm{10}}\:=\:\frac{\mathrm{2}{x}+\mathrm{1}}{\mathrm{2}{a}−\mathrm{2}{x}+\mathrm{1}}\: \\ $$$$\:\:\Rightarrow\:\mathrm{22}{a}−\mathrm{22}{x}+\mathrm{11}\:=\:\mathrm{20}{x}+\mathrm{10} \\ $$$$\:\:\Rightarrow\:\mathrm{42}{x}\:=\:\mathrm{22}{a}+\mathrm{1}\: \\ $$$$\:\:\Rightarrow\:{x}\:=\:\frac{\mathrm{22}{a}+\mathrm{1}}{\mathrm{42}}\: \\ $$
Commented by mr W last updated on 17/Apr/24

$${seems}\:{not}\:{true}. \\ $$
Answered by A5T last updated on 13/Apr/24

Commented by A5T last updated on 13/Apr/24

$${sx}\sqrt{\mathrm{3}}+\frac{{s}^{\mathrm{2}} \sqrt{\mathrm{3}}}{\mathrm{4}}=\mathrm{10}+\frac{{sx}\sqrt{\mathrm{3}}}{\mathrm{4}}+\frac{{sx}\sqrt{\mathrm{3}}}{\mathrm{2}}\Rightarrow\frac{{s}^{\mathrm{2}} \sqrt{\mathrm{3}}+{sx}\sqrt{\mathrm{3}}}{\mathrm{4}}=\mathrm{10} \\ $$$$\Rightarrow{s}^{\mathrm{2}} +{sx}=\frac{\mathrm{40}\sqrt{\mathrm{3}}}{\mathrm{3}}…\left({i}\right) \\ $$$$\left({s}−{x}\right){s}\sqrt{\mathrm{3}}+\frac{{s}^{\mathrm{2}} \sqrt{\mathrm{3}}}{\mathrm{4}}=\mathrm{11}+\frac{{s}\left({s}−{x}\right)\sqrt{\mathrm{3}}}{\mathrm{4}}+\frac{{s}\left({s}−{x}\right)\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\Rightarrow\frac{{s}\left({s}−{x}\right)\sqrt{\mathrm{3}}+{s}^{\mathrm{2}} \sqrt{\mathrm{3}}}{\mathrm{4}}=\mathrm{11}\Rightarrow\mathrm{2}{s}^{\mathrm{2}} −{sx}=\frac{\mathrm{44}\sqrt{\mathrm{3}}}{\mathrm{3}}…\left({ii}\right) \\ $$$$\left({i}\right)+\left({ii}\right)\Rightarrow{s}^{\mathrm{2}} =\frac{\mathrm{84}\sqrt{\mathrm{3}}}{\mathrm{9}}\Rightarrow{s}=\sqrt{\frac{\mathrm{28}\sqrt{\mathrm{3}}}{\mathrm{3}}} \\ $$$$\mathrm{2}×\left({i}\right)−\left({ii}\right)\Rightarrow{sx}=\mathrm{4}\sqrt{\mathrm{3}}\Rightarrow{x}=\mathrm{4}\sqrt{\mathrm{3}}×\frac{\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{28}\sqrt{\mathrm{3}}}}\approx\mathrm{1}.\mathrm{723} \\ $$
Answered by A5T last updated on 13/Apr/24

Commented by A5T last updated on 13/Apr/24

$$\frac{{s}^{\mathrm{2}} \sqrt{\mathrm{3}}}{\mathrm{4}}+\frac{{s}\left({s}−{x}\right)\sqrt{\mathrm{3}}}{\mathrm{2}}=\mathrm{11}+{s}\left({s}−{x}\right)×\frac{\sqrt{\mathrm{3}}}{\mathrm{4}} \\ $$$$\Rightarrow\frac{{s}^{\mathrm{2}} \sqrt{\mathrm{3}}}{\mathrm{4}}+\frac{{s}\left({s}−{x}\right)\sqrt{\mathrm{3}}}{\mathrm{4}}=\frac{{s}^{\mathrm{2}} \sqrt{\mathrm{3}}}{\mathrm{2}}−\frac{{sx}\sqrt{\mathrm{3}}}{\mathrm{4}}=\mathrm{11} \\ $$$$\Rightarrow\mathrm{2}{s}^{\mathrm{2}} −{sx}=\frac{\mathrm{44}\sqrt{\mathrm{3}}}{\mathrm{3}}…\left({i}\right) \\ $$$$\frac{{s}^{\mathrm{2}} \sqrt{\mathrm{3}}}{\mathrm{4}}+\frac{{sx}\sqrt{\mathrm{3}}}{\mathrm{2}}=\mathrm{10}+\frac{{sx}\sqrt{\mathrm{3}}}{\mathrm{4}}\Rightarrow{s}^{\mathrm{2}} \sqrt{\mathrm{3}}+{sx}\sqrt{\mathrm{3}}=\mathrm{40} \\ $$$$\Rightarrow{s}^{\mathrm{2}} +{sx}=\frac{\mathrm{40}\sqrt{\mathrm{3}}}{\mathrm{3}}…\left({ii}\right) \\ $$$$\left({i}\right)\&\left({ii}\right)\Rightarrow{x}\approx\mathrm{1}.\mathrm{723} \\ $$
