Question Number 206430 by cortano21 last updated on 14/Apr/24
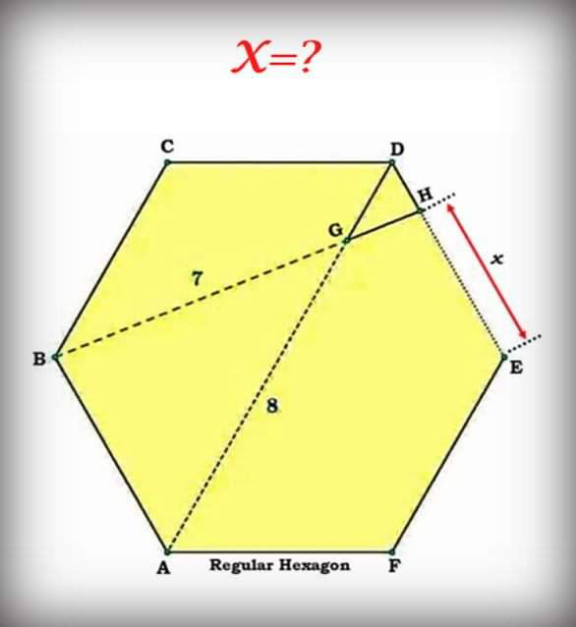
Answered by mr W last updated on 14/Apr/24

$${AB}={a},\:{say} \\ $$$$\mathrm{7}^{\mathrm{2}} ={a}^{\mathrm{2}} +\mathrm{8}^{\mathrm{2}} −\mathrm{2}×\mathrm{8}{a}\:\mathrm{cos}\:\mathrm{60}° \\ $$$${a}^{\mathrm{2}} −\mathrm{8}{a}\:+\mathrm{15}=\mathrm{0} \\ $$$$\left({a}−\mathrm{3}\right)\left({a}−\mathrm{5}\right)=\mathrm{0} \\ $$$${a}=\:\mathrm{5}\:{or}\:\mathrm{3}\:\left({rejected},\:{since}\:{AD}=\mathrm{2}{a}\:{must}\:\geqslant\mathrm{8}\right) \\ $$$${GD}=\mathrm{2}{a}−\mathrm{8}=\mathrm{2}×\mathrm{5}−\mathrm{8}=\mathrm{2} \\ $$$$\frac{{DH}}{{a}}=\frac{{GD}}{\mathrm{8}}\:=\frac{\mathrm{2}}{\mathrm{8}}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\Rightarrow{DH}=\frac{{a}}{\mathrm{4}}\:\Rightarrow{x}=\frac{\mathrm{3}}{\mathrm{4}}{a}=\frac{\mathrm{15}}{\mathrm{4}}\:\checkmark \\ $$
Answered by A5T last updated on 14/Apr/24

$${AD}=\mathrm{2}{a}\Rightarrow{DG}=\mathrm{2}{a}−\mathrm{8} \\ $$$$\frac{\mathrm{7}}{{GH}}=\frac{\mathrm{8}}{{DG}}\Rightarrow{GH}=\frac{\mathrm{7}\left({a}−\mathrm{4}\right)}{\mathrm{4}} \\ $$$$\frac{{a}}{{DH}}=\frac{\mathrm{7}}{{GH}}\Rightarrow{DH}=\frac{{a}\left({a}−\mathrm{4}\right)}{\mathrm{4}}\Rightarrow{x}=\frac{\mathrm{8}{a}−{a}^{\mathrm{2}} }{\mathrm{4}} \\ $$$${a}^{\mathrm{2}} +\mathrm{8}^{\mathrm{2}} −{a}×\mathrm{8}=\mathrm{49}\Rightarrow\mathrm{8}{a}−{a}^{\mathrm{2}} =\mathrm{15}\Rightarrow{x}=\frac{\mathrm{15}}{\mathrm{4}} \\ $$
