Question-206466

Question Number 206466 by cortano21 last updated on 15/Apr/24

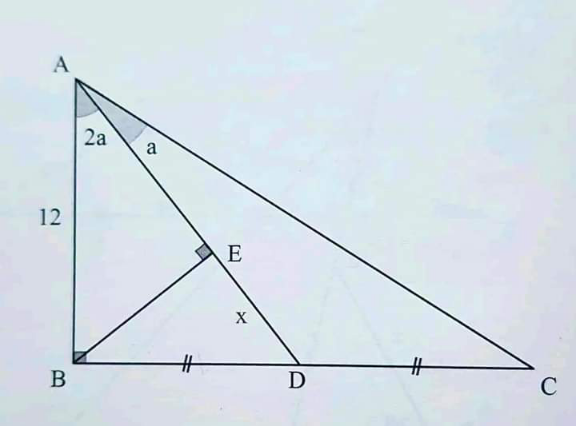
Commented by cortano21 last updated on 15/Apr/24

$$\:\: \\ $$

Answered by mr W last updated on 15/Apr/24

tan 3α=2 tan 2α ((tan α(3−tan^2 α))/(1−3 tan^2 α))=((4 tan α)/(1−tan^2 α)) tan^4 α+8 tan^2 α−1=0 tan^2 α=(√(17))−4 x=12 sin 2α tan 2α=((48 tan^2 α)/(1−tan^4 α)) =((48((√(17))−4))/( 1−((√(17))−4)^2 ))=6

$$\mathrm{tan}\:\mathrm{3}\alpha=\mathrm{2}\:\mathrm{tan}\:\mathrm{2}\alpha \\ $$$$\frac{\mathrm{tan}\:\alpha\left(\mathrm{3}−\mathrm{tan}^{\mathrm{2}} \:\alpha\right)}{\mathrm{1}−\mathrm{3}\:\mathrm{tan}^{\mathrm{2}} \:\alpha}=\frac{\mathrm{4}\:\mathrm{tan}\:\alpha}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:\alpha} \\ $$$$\mathrm{tan}^{\mathrm{4}} \:\alpha+\mathrm{8}\:\mathrm{tan}^{\mathrm{2}} \:\alpha−\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{tan}^{\mathrm{2}} \:\alpha=\sqrt{\mathrm{17}}−\mathrm{4} \\ $$$${x}=\mathrm{12}\:\mathrm{sin}\:\mathrm{2}\alpha\:\mathrm{tan}\:\mathrm{2}\alpha=\frac{\mathrm{48}\:\mathrm{tan}^{\mathrm{2}} \:\alpha}{\mathrm{1}−\mathrm{tan}^{\mathrm{4}} \:\alpha} \\ $$$$\:\:\:=\frac{\mathrm{48}\left(\sqrt{\mathrm{17}}−\mathrm{4}\right)}{\:\mathrm{1}−\left(\sqrt{\mathrm{17}}−\mathrm{4}\right)^{\mathrm{2}} }=\mathrm{6} \\ $$

Facebook Tweet Pin

Question-206466

Leave a Reply Cancel reply