Question Number 206554 by cortano21 last updated on 18/Apr/24
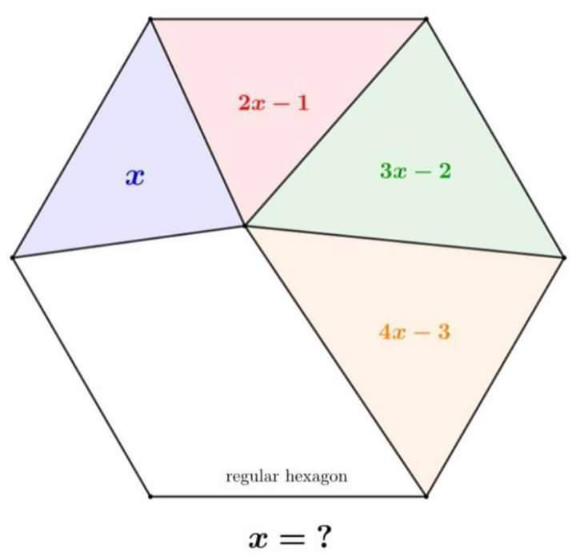
Answered by starsouf last updated on 18/Apr/24

$$ \\ $$
Answered by mr W last updated on 18/Apr/24

Commented by mr W last updated on 18/Apr/24

$${S}={area}\:{of}\:{hexagon} \\ $$$${x}+\left(\mathrm{4}{x}−\mathrm{3}\right)=\frac{{S}}{\mathrm{3}}=\left(\mathrm{2}{x}−\mathrm{1}\right)+\left(\mathrm{3}{x}−\mathrm{2}\right) \\ $$$$\mathrm{2}{x}−\mathrm{1}+{B}=\frac{{S}}{\mathrm{3}}\:\Rightarrow{B}=\mathrm{3}{x}−\mathrm{2} \\ $$$$\mathrm{3}{x}−\mathrm{2}+{A}=\frac{{S}}{\mathrm{3}}\:\Rightarrow{A}=\mathrm{2}{x}−\mathrm{1} \\ $$$$\left(\mathrm{4}{x}−\mathrm{3}\right)−{x}=\frac{{ah}}{\mathrm{2}}\:\Rightarrow\mathrm{6}{x}−\mathrm{6}={ah} \\ $$$$\mathrm{2}\left(\mathrm{3}{x}−\mathrm{2}\right)+\left(\mathrm{4}{x}−\mathrm{3}\right)−\mathrm{2}\left(\mathrm{2}{x}−\mathrm{1}\right)−{x}=\frac{\mathrm{2}{ah}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{5}{x}−\mathrm{5}={ah} \\ $$$$\mathrm{6}{x}−\mathrm{6}=\mathrm{5}{x}−\mathrm{5} \\ $$$$\Rightarrow{x}=\mathrm{1}\:\checkmark \\ $$
Commented by A5T last updated on 16/May/24

$$\mathrm{2}\left(\mathrm{3}{x}−\mathrm{2}\right)+\left(\mathrm{4}{x}−\mathrm{3}\right)−\mathrm{2}\left(\mathrm{2}{x}−\mathrm{1}\right)−{x}=\frac{\mathrm{2}{ah}}{\mathrm{2}} \\ $$$${I}\:{guess}\:{this}\:{should}\:{be}: \\ $$$$\mathrm{2}\left(\mathrm{3}{x}−\mathrm{2}\right)+\left(\mathrm{4}{x}−\mathrm{3}\right)−\mathrm{2}\left(\mathrm{2}{x}−\mathrm{1}\right)−{x}=\mathrm{2}\left(\frac{\mathrm{2}{ah}}{\mathrm{2}}\right)=\mathrm{2}{ah} \\ $$$$\Rightarrow\mathrm{5}{x}−\mathrm{5}=\mathrm{2}{ah}\Rightarrow\mathrm{12}{x}−\mathrm{12}=\mathrm{5}{x}−\mathrm{5} \\ $$$$\Rightarrow{x}=\mathrm{1} \\ $$
Commented by mr W last updated on 16/May/24

$${i}\:{think} \\ $$$$\mathrm{2}\left(\mathrm{3}{x}−\mathrm{2}\right)+\left(\mathrm{4}{x}−\mathrm{3}\right)−\mathrm{2}\left(\mathrm{2}{x}−\mathrm{1}\right)−{x}=\frac{\mathrm{2}{ah}}{\mathrm{2}} \\ $$$${is}\:{right}. \\ $$$${base}\:=\mathrm{2}{a} \\ $$$${hight}\:={h} \\ $$$${area}\:=\frac{\mathrm{2}{a}×{h}}{\mathrm{2}} \\ $$
Commented by A5T last updated on 16/May/24

$${I}\:{understand}\:{that}\:{the}\:{area}\:{is}\:\frac{\mathrm{2}{a}×{h}}{\mathrm{2}}={ah}. \\ $$$${But}\:\mathrm{2}\left(\mathrm{3}{x}−\mathrm{2}\right)+\mathrm{4}{x}−\mathrm{3}−\mathrm{2}\left(\mathrm{2}{x}−\mathrm{1}\right)\:{is}\:{twice}\:{of}\:{that}. \\ $$$${If}\:{one}\:{applies}\:{this}\:{method}\:{to}\:{your}\:{latest}\:{question}, \\ $$$${one}\:{would}\:{get}\:?=\mathrm{3}. \\ $$
Commented by mr W last updated on 16/May/24

$${you}\:{are}\:{right}.\:{it}\:{should}\:{be} \\ $$$$\mathrm{2}\left(\mathrm{3}{x}−\mathrm{2}\right)+\left(\mathrm{4}{x}−\mathrm{3}\right)−\mathrm{2}\left(\mathrm{2}{x}−\mathrm{1}\right)−{x}=\mathrm{2}×\frac{\mathrm{2}{ah}}{\mathrm{2}} \\ $$
